Cum se măsoară frecvența înaltă și ciclul de funcționare, simultan, folosind un microcontroler .: 4 pași

2024 Autor: John Day | [email protected]. Modificat ultima dată: 2024-01-30 11:44

Știu ce părere aveți: "Huh? Există o mulțime de Instrucțiuni despre cum să utilizați microcontrolerele pentru a măsura frecvența semnalului. Căscat". Dar așteaptă, există o noutate în aceasta: descriu o metodă de măsurare a frecvențelor mult mai mari decât poate suporta un microcontroler (MCU) și ciclul de funcționare al semnalului - toate în același timp!

Gama de frecvență a dispozitivului se întinde de la ~ 43 Hz la ~ 450 kHz, în timp ce ciclul de funcționare variază de la 1% până la 99%.

Permiteți-mi să explic partea "poate suporta": un MCU măsoară perioada unui semnal de undă pătrată, T, urmărind timpul dintre două evenimente de tranziție ulterioare. De exemplu, tensiunea joasă până la înaltă sare pe unul dintre pinii I / O. O face numărând numărul de impulsuri ale propriului ceas intern. Naiv, limita superioară pentru frecvențele măsurate ar trebui să respecte teorema de eșantionare Nyqvist-Shannon; adică, ar fi aproximativ egal cu jumătatea frecvenței ceasului MCU-urilor. În realitate, limita este mult, mult mai mică, deoarece MCU trebuie să execute cod pentru a gestiona întreruperile, pentru a salva variabile, pentru a efectua operații aritmetice, pentru a afișa rezultatele etc. aproximativ 106. Prin urmare, limita superioară a intervalului de frecvență măsurabilă în acest caz ar fi 48, 000/212/2 = 226,4 kHz.

În timp ce MCU măsoară perioada semnalului, poate determina, de asemenea, lățimea impulsului său, P: timpul de tensiune a semnalului care rămâne ridicat. Cu alte cuvinte, timpul dintre tranzițiile de la scăzut la înalt și de la scăzut la scăzut. Ciclul de funcționare al semnalului este apoi definit ca următorul procent:

Taxă = 100% * P / T

La fel ca în cazul frecvenței, există o limită practică a lățimii impulsului. Folosind exemplul de mai sus, 106 cicluri de ceas ar limita lățimea impulsului la cel puțin 2,21 microsecunde. Sau, nu mai puțin de 50% la 226,4 kHz.

Una dintre modalitățile de creștere a limitei superioare de frecvență a semnalelor de undă pătrată este aplicarea separatoarelor digitale care utilizează flip-flops. Împărțirea frecvenței de intrare cu n ar extinde intervalul superior măsurabil de n ori. Aceasta este o veste minunată, separatoarele digitale au un defect fundamental: semnalul divizat pierde informațiile despre lățimea impulsului (și ciclul de funcționare)! Datorită modului în care funcționează separatoarele, producția lor are întotdeauna un ciclu de funcționare de 50%. Păcat…

Cu toate acestea, în paginile următoare voi arăta cum să împart digital frecvența și să păstrez lățimea originală a impulsului, permițându-mi să măsoară semnalele cu mult peste limitele impuse de numărarea directă.

Pasul 1: Divizia de frecvență digitală

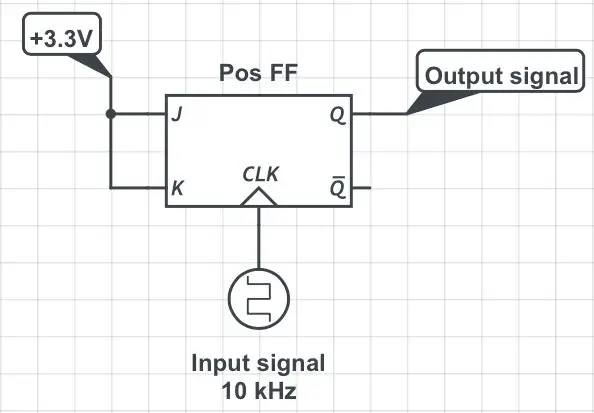
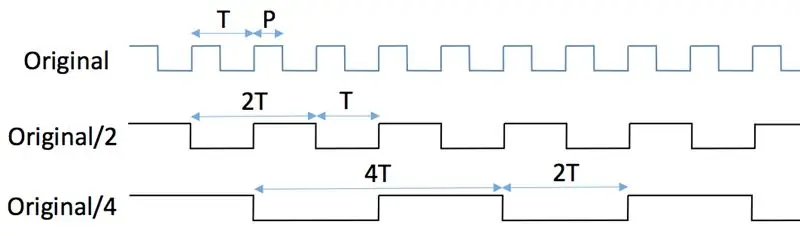
Divizoarele de frecvență digitale tradiționale folosesc flip-flops; acest tutorial explică frumos principiile cum se construiesc separatoare folosind flip-flops-urile standard JK. Aceasta rezolvă problema frecvențelor de intrare prea mari pentru MCU, dar are un dezavantaj major: semnalul împărțit are un ciclu de funcționare de 50%, indiferent de sarcina semnalului de intrare! Pentru a vedea de ce este cazul, uitați-vă la primele două figuri. Semnalul original cu perioada T și lățimea impulsului P este introdus în pinul de ceas al unui flip-flop JK, în timp ce pinii J și K sunt menținuți în permanență la înălțime (prima figură). Logica de 3.3V este asumată pe tot parcursul. Să presupunem că flip-flop-ul este declanșat de marginea pozitivă (adică în creștere) a ceasului. În aceste condiții, modificările stării pinului de ieșire („flip” și „flops” individuale) apar de fiecare dată când pinul de ceas trece de la cel mai mic la cel mai mare. Ceasul de tranziție de la înalt la scăzut (adică marginea negativă) este complet ignorat. Vezi a doua figură. Pinul de ieșire, Q, emite un semnal a cărui perioadă este de două ori mai lungă decât perioada inițială, adică frecvența sa este redusă la jumătate. Lățimea impulsului de ieșire este întotdeauna egală cu T. În consecință, lățimea impulsului original, P, se pierde.

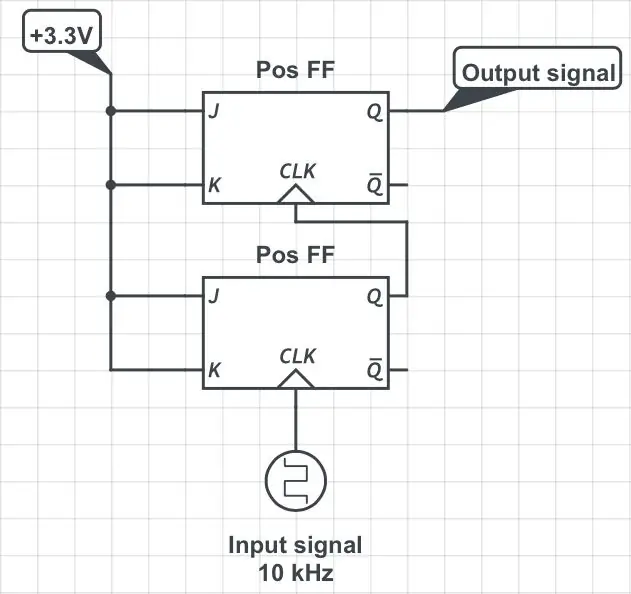
Adăugarea unui alt flip-flop JK într-o configurație prezentată în a treia figură împarte frecvența inițială cu 4. Adăugarea mai multor flip-flop în același mod secvențial împarte frecvența prin puterile ulterioare de 2: 8, 16, 32 etc.

Problemă: cum se împarte frecvența unei unde pătrate păstrând lățimea pulsului?

Ideea este să adăugați în mod corespunzător un flip-flop JK declanșat de margine negativă la mix. Să-i spunem „Neg FF”; vezi a patra figură. Aici, „în mod corespunzător” înseamnă că pinii J și K ai noului flip-flop sunt legați de pinii de ieșire Q și Qbar, respectiv, ai divizorului cu 4 („Pos FF”) ilustrat în figura anterioară. (Aici, „bară” este bara orizontală peste simbolul Q care indică negarea logică.) Pentru a vedea ce realizează acest lucru, aruncați o privire la tabelul de funcții al „Neg FF” din figura a cincea: pinii de ieșire ai lui Neg, Q și Qbar, reflectă starea pinilor de intrare, respectiv J și K. Ceea ce înseamnă că reflectă starea Pos 'Q și Qbar. Dar acțiunea flip-flop a lui Neg trebuie să aștepte marginea negativă a semnalului original, care ajunge la momentul P după marginea pozitivă. Aha!

Formele de undă rezultate sunt ilustrate în a șasea figură. „Pos Q” emite semnal la 1/4 de frecvență, „Pos Qbar” este invers, „Neg Q” urmează „Pos Q” modificat de lățimea impulsului P și „Neg Qbar” este inversul acestuia. Puteți verifica dacă AND-ul logic al „Pos Qbar” și „Neg Q” produce un tren de impulsuri caracterizat prin lățimea originală a impulsului P și 1/4 din frecvență. Bingo!

La început am folosit exact acest semnal de ieșire pentru a alimenta MCU. Cu toate acestea, sa dovedit a fi problematic pentru lățimi de impuls foarte scurte, din cauza limitărilor de 106 cicluri ale MCU menționate în Introducere. Am rezolvat această mică problemă alegând o altă ieșire: „Pos Qbar” ȘI „Neg Qbar”. O privire asupra formelor de undă ar trebui să vă convingă că lățimea impulsului acestei forme de undă, P ', variază între T și 2T în loc de intervalul (0, T) pentru P. P poate fi ușor recuperat din P' prin:

P = 2T - P '

Pasul 2: Hardware recomandat

Îmi place cu adevărat relativ nou-venit la pasionații de electronice: MCU-urile Atmel SAM D21 bazate pe procesorul ARM Cortex M0 + pe 32 de biți care funcționează la o rată de ceas de 48 MHz, mult mai mare decât Atmels mai vechi. Pentru acest proiect am cumpărat:

• Placa MCU ItsyBitsy M0 Express de la Adafruit
• Am avut o baterie reîncărcabilă LiPo de la Adafruit
• Afișaj monocrom 128x32 SPI OLED (l-ați ghicit: Adafruit)
• Flip-flop JK SN74HC109 cu declanșare pozitivă pe margine pozitivă de la Texas Instruments
• Flip-flop JK SN74HC112 declanșat cu margine negativă duală de la Texas Instruments
• Cvadruplă ȘI poartă CD74AC08E de la Texas Instruments
• Cvadruplă SAU poartă CD74AC32E de la Texas Instruments

Pasul 3: Circuitul

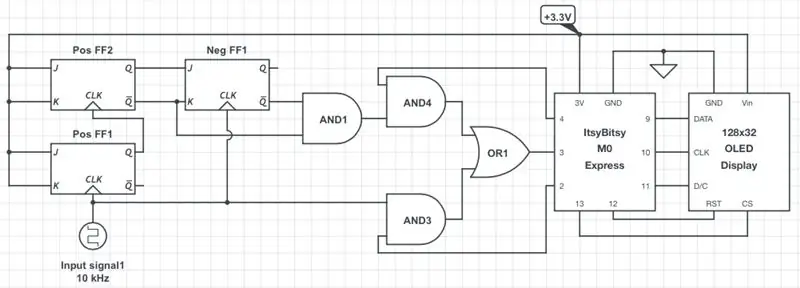
Prima figură prezintă o schemă simplificată a contorului de frecvență / sarcină. Logica CMOS de 3,3 V este asumată pe tot parcursul. În consecință, amplitudinea undei pătrate de intrare trebuie să fie între V-ul corespunzător_IH nivel (adică, 2 V) și 3,3 V. Dacă nu, trebuie să îl ridicați în sus sau în jos corespunzător. În majoritatea cazurilor ar fi suficient un simplu divizor de tensiune. Dacă doriți să proiectați versiunea contorului la un nivel logic diferit, atunci trebuie să utilizați un alt microcontroler (MCU), baterie și un afișaj care funcționează la nivelul dorit. Porțile logice și flip-flop-urile utilizate în acest proiect funcționează cu niveluri logice între 2 V și 6 V și ar trebui să fie OK în majoritatea cazurilor.

După cum se arată, ItsyBitsy MCU folosește pinii 9-13 pentru a comunica cu afișajul prin intermediul protocolului SPI software. Pinul de 3V furnizează energie întregului circuit. Pinul digital de intrare 3 acceptă semnalul analizat, în timp ce pinii 2 și 4 controlează sursa semnalului: fie semnal direct care trece prin poarta AND3 (frecvențe de intrare scăzute), fie semnal împărțit la 4 prin poarta AND4 (frecvențe de intrare înalte), așa cum este descris în Pasul 2 Codul, discutat în pasul următor, detectează automat intervalul de frecvență de intrare și comută în mod corespunzător sursa de semnal.

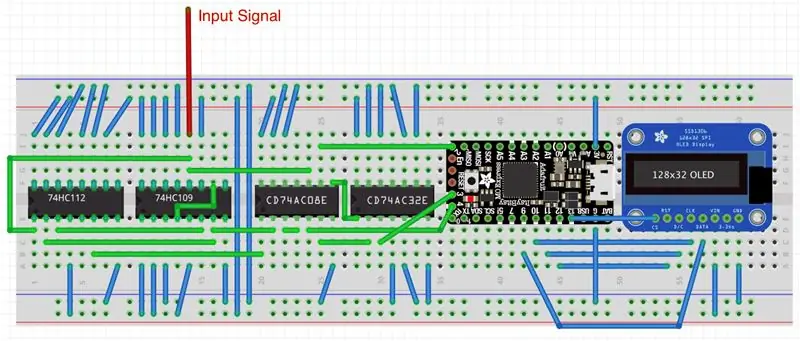
Schema nu arată adevărata complexitate a conexiunilor cu cipuri digitale. Cea de-a doua imagine arată cum ar arăta proiectul pe o placă de calcul. Semnalul de intrare vine printr-un fir roșu la pinul 2CLK al flip-flopului cu margine pozitivă duală. ATENȚIE: În mod normal, toate știfturile J și K ale acestui flip-flop ar trebui menținute sus, dar SN74HC109 are în special știftul Kbar - un știft K inversat - în schimb. Prin urmare, acest știft trebuie să fie împământat! Primul flip-flop negru de margine din SN74HC112 are pinii 1K și 1J conectați la pinii 1Q și 1Qbar ai SN74HC109. Al doilea flip-flop din SN74HC112 nu este utilizat și pinii de intrare (2K, 2J, 2CLRbar) sunt împământați. Toți ceilalți pini suplimentari PREbar (preset) și CLRbar (clear) din toate flip-flop-urile trebuie să fie conectați la high logic. Ceasurile și pinii de ieșire neutilizați sunt lăsați neconectați. În mod similar, pinii de intrare neutilizați din toate porțile sunt împământați, în timp ce pinii de ieșire neutilizați sunt lăsați neconectați. Așa cum am discutat în „Invisible Killer of the Phone Ring” instructabil, împământarea pinilor de intrare neutilizați ai cipurilor logice elimină oscilațiile aleatorii și economisește energia bateriei.

Pasul 4: Codul și măsurarea frecvențelor joase

Bineînțeles, toată acțiunea se întâmplă în codul legat mai jos. Când intrarea de intrare pe pinul 3 trece de la digital la minim, MCU începe să numere impulsurile ceasului său intern de 48 MHz. Notează momentul tranziției de la mare la scăzut și continuă numărul până la următorul comutator de scăzut la scăzut, când repornește din nou întregul proces. Primul număr reprezintă lățimea impulsului, în timp ce întregul număr reprezintă perioada semnalului. Și acesta este întregul secret.

CPU notează aceste tranziții prin întreruperi hardware. SAMD21 are mai multe ceasuri; codul meu folosește TC3 one. Inițial, am început citind foaia de date a lui M0 pentru a face eforturi mari în codificarea manipulatorului de întreruperi, dar în curând am descoperit un cod foarte legat în postările Arduino Forum ale utilizatorilor electro_95, MartinL și Rucus a căror contribuție este recunoscută în mod corespunzător. Am încorporat și modificat codul lor combinat în al meu; economisindu-mă mult timp!

După cum am menționat anterior, rezoluția semnalului este limitată de ~ 106 cicluri CPU pentru a executa cod între întreruperi. Diviziunea digitală cu conservarea lățimii impulsurilor are grijă de frecvențele înalte. Frecvențele joase, pe de altă parte, reprezintă o altă provocare: deoarece contorul de ceas TC3 are o lungime de 16 biți, acesta se revarsă după trecerea limitei de 65, 536 de numărătoare. Se poate rezolva această situație adăugând o întrerupere de depășire, dar a ales o altă soluție: TC3 poate utiliza un ceas CPU precalificat (adică împărțit software) în locul celui hardware de 48 MHz. Astfel, dacă perioada semnalului se apropie de limita de revărsare, codul poate instrui TC3 să utilizeze numărările de 24 MHz pentru perioada următoare și, voila, contorul scade sub 32, 768 de numărări. Pentru frecvențe chiar mai mici, TC3 poate fi instruit să numere impulsuri de 12 MHz etc. Precalificatorul corespunzător este determinat automat pe baza frecvenței semnalului, cu histerezis, pentru a menține contorul TC3 în limita de deversare. Ca urmare, capătul inferior al gamei dispozitivului este de aproximativ 43 Hz.

Sunteți binevenit să codificați codul și să îl utilizați în proiectul dvs., dar vă rugăm să menționați sursa acestuia la publicarea rezultatelor.

Link către cod.