Sumarea recursivă a unui tablou în Java: 9 pași

2024 Autor: John Day | [email protected]. Modificat ultima dată: 2024-01-30 11:42

Recursivitatea este o procedură foarte utilă și eficientă în timp, care poate rezolva rapid o problemă cu foarte puțin cod. Recursivitatea implică metoda pe care o creați numindu-se ea însăși scurtând problema inițială.

Pentru acest exemplu, vom însuma o matrice de 10 numere întregi, dar dimensiunea ar putea fi de orice lungime.

Provizii

Ar trebui să cunoașteți sintaxa de bază Java și să aveți IDE-ul sau un editor de text pentru a vă scrie codul pentru această sarcină.

Pasul 1: Configurați-vă metoda principală

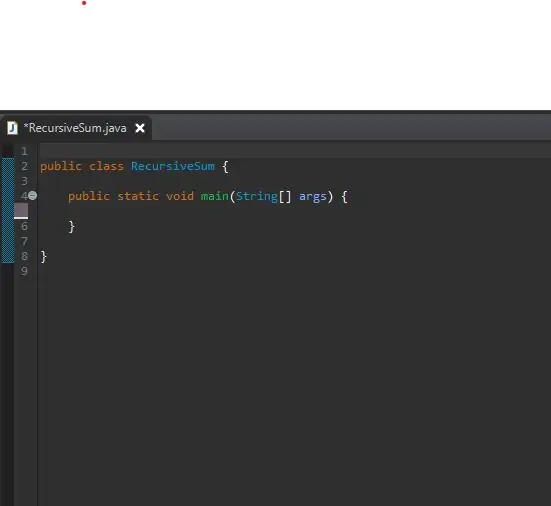
Pentru început, configurați metoda principală într-o clasă nou creată. Mi-am numit clasa RecursiveSum. Aici veți crea matricea de numere întregi și veți apela metoda recursivă.

Pasul 2: Creați antetul metodei recursive

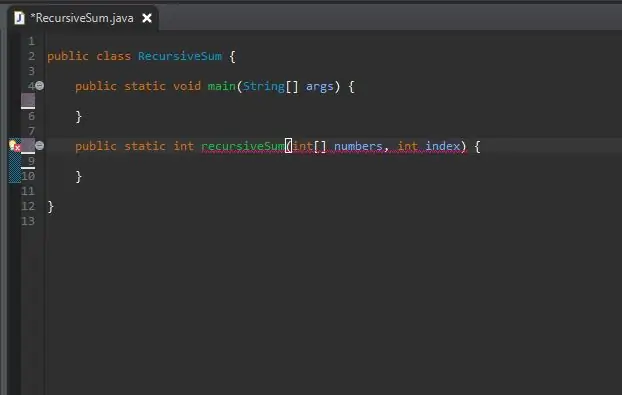
În afara metodei principale, creați antetul metodei pentru metoda recursivă.

Metoda este statică, deoarece nu va necesita un obiect pentru a o folosi.

Tipul returnat este int, deoarece matricea pe care o vom folosi va fi completă pe numere întregi. Cu toate acestea, acest lucru poate fi schimbat cu orice tip de număr conține matricea.

Am denumit metoda mea recursiveSum, care va lua doi parametri; o serie de numere întregi și indexul pe care îl vom adăuga la sumă. Am numit acești parametri numere și respectiv index.

Veți vedea erori chiar acum și este în regulă. Vor fi remediate mai târziu.

Pasul 3: Creați-vă Kicker-ul / Carcasa de bază

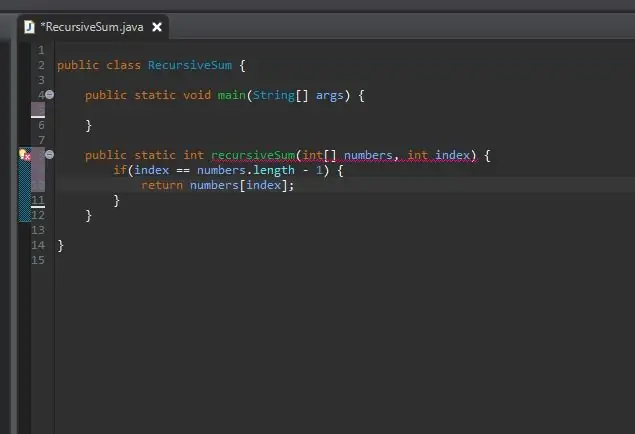
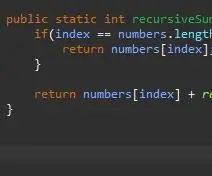
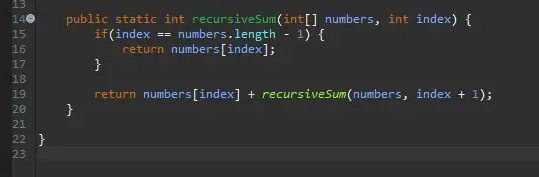
O metodă recursivă are nevoie de un caz kicker / bază. Aceasta este condiția care va împiedica metoda dvs. să se numească infinit. Acest caz de bază poate fi considerat cel mai simplu caz pe care îl vom întâlni. În acest caz, cazul de bază va fi atunci când suntem la sfârșitul matricei noastre. Dacă indicele curent este egal cu lungimea matricei (minus 1 pentru că matricile încep să se numere de la 0 nu 1), suntem la sfârșit și returnăm pur și simplu acel element la acel index.

Pasul 4: Pasul recursiv

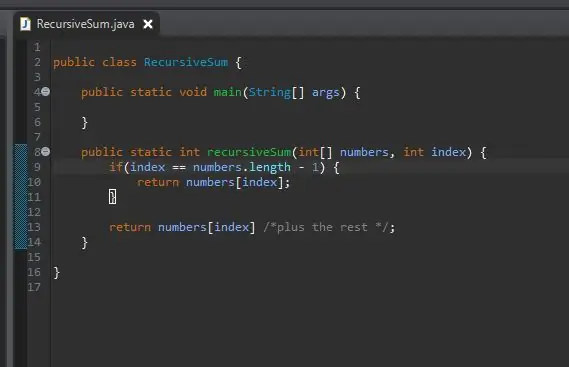
Odată ce avem cazul nostru de bază, următorul pas este pasul nostru recursiv. Aici se întâmplă magia. Am tratat cazul când indicele nostru este egal cu ultimul element din matricea noastră. Ce se întâmplă dacă nu suntem la ultimul element din matricea noastră? Ce se întâmplă dacă i-am putea spune pur și simplu să adauge elementul nostru curent plus următorul? În cele din urmă vom atinge sfârșitul matricei noastre, iar cazul nostru de bază va avea efect.

Pentru a realiza acest lucru, returnăm pur și simplu indexul curent și „adăugăm restul” matricei.

Pasul 5: Scurtați problema

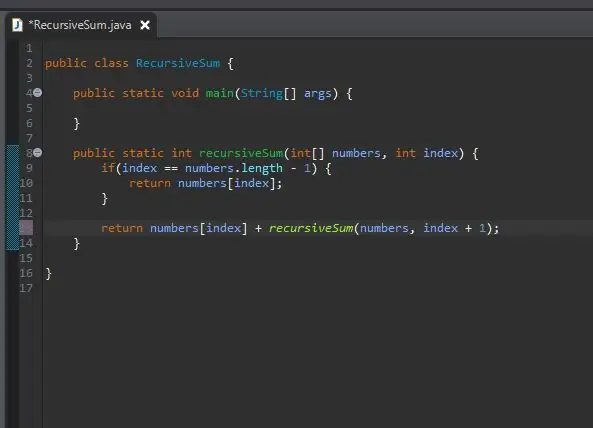
Cum simplificăm „adăugăm restul”? Avem deja o metodă care va adăuga un anumit element; metoda noastră recursiveSum ()! Îl putem apela din nou, dar schimbăm indexul pe care îl însumăm.

Trecem în aceeași matrice pe care o procesăm, dar trecem în următorul index din indexul nostru curent. Facem acest lucru prin simpla adăugare a unuia la indexul nostru actual așa cum se arată.

Pasul 6: Creați matricea numerelor întregi

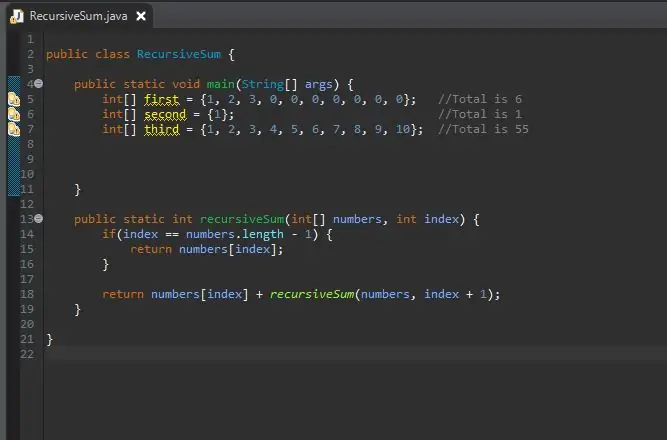
Acum că metoda noastră de însumare recursivă este completă, putem crea matricea pe care o vom procesa. Această matrice va fi în blocul nostru principal de metode.

Puteți face dimensiunea matricei atâta timp cât doriți. Am creat câteva tablouri diferite cu dimensiuni și valori diferite pentru a arăta că funcționează nu doar pe o singură dimensiune.

Pasul 7: Apelați metoda cu matricele dvs

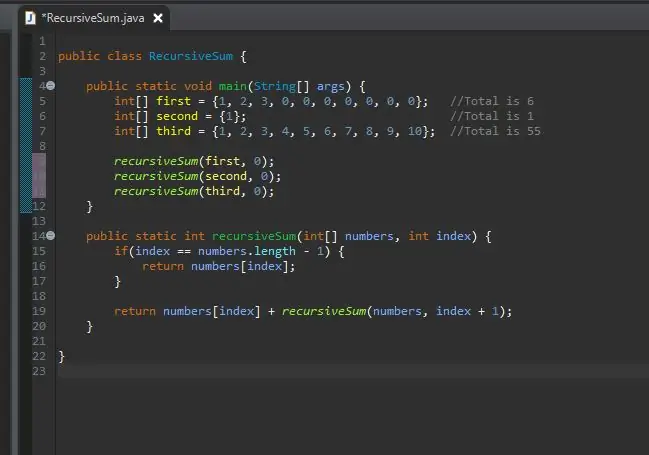
Acum puteți apela metoda recursivă și îi puteți transmite aceste matrice. Acum puteți rula programul.

Pasul 8: tipăriți rezultatele

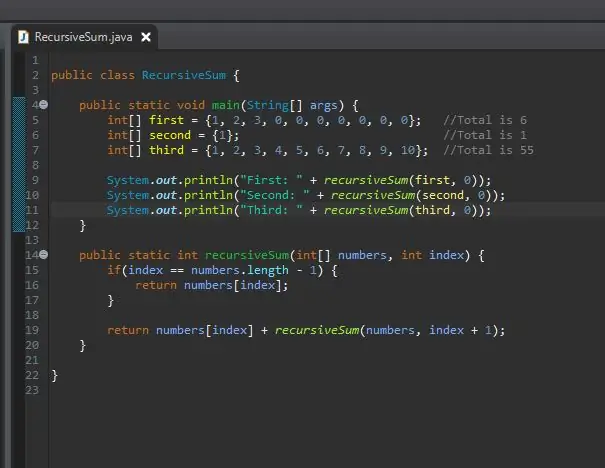
Nu s-a intamplat nimic. De ce? Suma recursivă returnează un număr întreg, dar nu am făcut nimic cu acest număr întreg. Și-a făcut treaba, dar nu putem vedea rezultatul. Pentru a vedea rezultatul, îl imprimăm pur și simplu așa. După ce rulați acest lucru, ar trebui să vedeți rezultatele pentru fiecare dintre matricile dvs.

Pasul 9: Felicitări

Ați finalizat o funcție recursivă. Simțiți-vă liber să modificați dimensiunea matricelor. Dacă îl testați, veți observa că se blochează când aveți o matrice goală. Nu am luat în considerare acest lucru, dar acesta este un mod excelent de a vă îmbunătăți metoda recursivă.