Cuprins:
- Pasul 1: Importați bibliotecile
- Pasul 2: Evalúa La Función
- Pasul 3: Asigna Variables De Las Coordenadas
- Pasul 4: Construcție Del Trapecio Según Coordenadas Y Función
- Pasul 5: Calcular El Área Del Trapecio Dentro De La Función
- Pasul 6: Gráfica En Pyplot
- Pasul 7: Organizația La Gráfica
- Pasul 8: ¡Lo Lograste
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:43.
- Modificat ultima dată 2025-01-23 15:04.
Antes that nada, for developar this program debes installar the platform Python from your oficial page:. Cel mai recomandabil este instalarea versiunii 2.7.12 de 64 de biți.
Pasul 1: Importați bibliotecile

Acest program necesită două biblioteci în cadrul programului: matplotlib.pyplot y pylab. În foto adjuntă acest pas se poate vedea că făcând uz de comenzi de la, import și ca programul să poată accesa informația celor două biblioteci utilizate pentru acest program.
din import pylab
importați matplotlib.pyplot ca plt
IMPORTANTE: ¡POR FAVOR NO PONGAS TILDES EN NINGUNA PALABRA NI NINGÚN SÍMBOLO DEL ESPAÑOL! DE LO CONTRARIO SE CERRARÁ EL PROGRAMA Y NO SE GUARDARÁN LOS CAMBIOS QUE HICISTE
Pasul 2: Evalúa La Función

Hay ciertas cosas que no puedes calcular sin saber ciertos data that the program no te can dar, a less that le preguntes to user (es say el that va a use the program after de su creation) the values of ciertas variables; în acest caz trebuie să întrebăm utilizatorului pentru funcția la care le-ați calcularea zonei.
Pentru a întreba utilizatorul pentru tipul de funcție, trebuie să facem uz de comenzi stream (str) și input. stream es un comando que permite introducir variables algebraicas (as "x" y "y") dentro de un conjunto numérico y que se entiendan como números desconocidos dentro de la ecuación, es decir que permite calcular, por ejemplo, x ^ 2 + 5 y que entienda a "x" ca un număr care nu se cunoaște. Por otro lado, input permite ca valoarea să se introducă atunci când programul se pregătește pentru variabila mare, pe care îl aduc pentru restul programului. Funcția linspace sirve pentru restrângerea valorilor eje a indicatelor în interiorul parintezei.
În acest caz, trebuie să definească variabila "y" prin mediu de o funcție
y = str (intrare ("f (x) ="))
x = np.linspace (0, 10) def f (x): return round (eval (y), 2)
Pasul 3: Asigna Variables De Las Coordenadas

Pentru că coordonatele carteziene se vor grafica, este necesar ca programul să se prezinte la utilizatorul valorilor care să ia funcția în eje x. Dado que estos son valores valores enteros, se debe volver a usar input, que permite que el valor que introduce cuando el programa pregunte por la variable sea el que se aducă pentru restul programului. Pentru că programul pregătește variabilele când pongasele funcționează, se folosesc print pentru că întrebarea apareză în ventana SHELL. În acest caz, se necesită să știe cele două valori ale x și restricția domeniului.
Recuerda que el dominio son los valores del eje x într-o funcție.
#valores de las coord. y limite del dominiox1 = float (input ("Cual es la coordenada x?")) x2 = float (input ("Cual es la coordenada x?")) dom = int (input ("Hasta donde se restringe el domino?")))
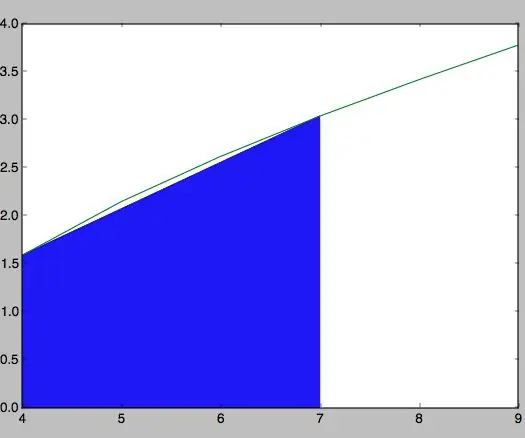
Pasul 4: Construcție Del Trapecio Según Coordenadas Y Función

Pentru a construi poligonul, deja aveți valorile care aduc funcția în x. Ahora, pentru valorile de y y (x1, 0) y (x2, 0), se atribuie variabilele y = f (x) și alt nume pentru anterior menționate.
#coordenadas para construcciona = (x1, 0) b = (x2, 0) y1 = f (x1) y2 = f (x2)
print ("De acord cu datele anterioare, trapul are coordonate:", (x1, y1), (x2, y2), a, b)
Pasul 5: Calcular El Área Del Trapecio Dentro De La Función
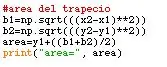
Pentru acest pas, trebuie să ai în cont la forma del trapecio, se spune, că are două baze și înălțimea. Las bases en este caso se obtienen por medio de la raíz cuadrada de la resta de los valores de x1 y x2 al cuadrado. Lo mismo ocurre para los valores de y1 y y2.
Pentru a salva suprafața totală, este suma de înălțime și bazele peste două.
#area del trapeciob1 = np.sqrt (((x2-x1) ** 2)) b2 = np.sqrt (((y2-y1) ** 2)) area = y1 + ((b1 + b2) / 2) print ("zonă =", zonă)
Pasul 6: Gráfica En Pyplot

#para que la function se grafique en pyplot
ejex =
ejey =
pentru i în interval (int (x1), dom):
ejex.append (i) ejey.append (f (i))
Pentru a cărei funcție se va grafica că asignează ejecțiile x & y, dar cum sunt deja multe variabile cu esențe, nu sunt atribuite câteva identități ca ejecții și alte variabile. El condițional pentru i in range organizează funcția de acord cu parametrii stabiliți la începutul programului.
Pasul 7: Organizația La Gráfica

x = [x1, x1, x2, x2, x1] y = [0, y1, y2, 0, 0]
plt.plot (x, y)
plt.plot (ejex, ejey) plt.fill_between (x, y) plt.show ()
În acest pas se organizează coordonatele de mod care coincid cu grafica în sus respectivi ejes. Por otro lado, es donde se rellena el espacio del trapecio en donde se va a calcular el área y se muestra la gráfica.
Pasul 8: ¡Lo Lograste
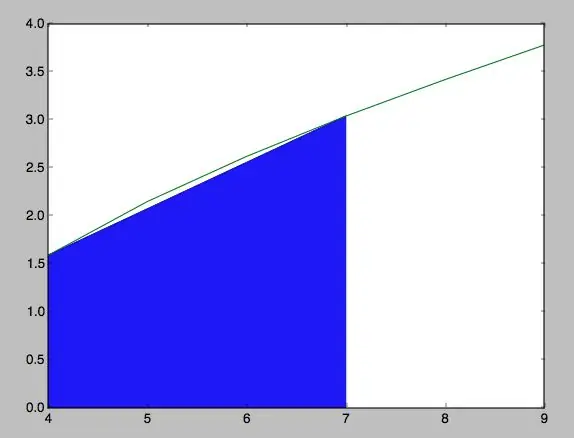
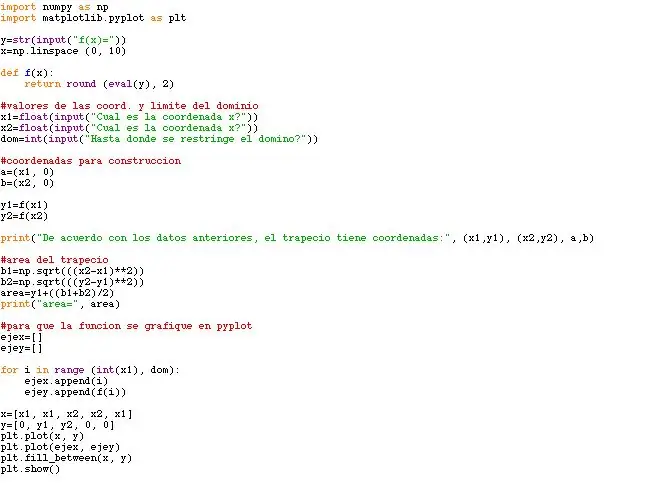

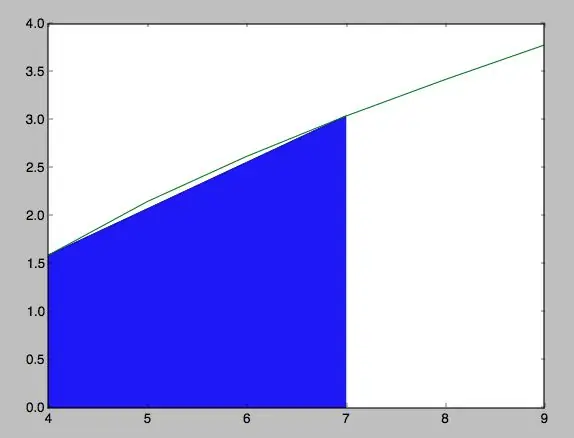
După ce a urmărit toți pașii, găsești că programul tău trebuie să fie foarte asemănător a ceea ce se află în fotografiile adjuntate. Obviamente, valorile de coordonate și funcția variază după cum tu vreau să puni, și pentru ende, zona și forma formei curbei.
Recomandat:
Como Crear Un Programa En Python Que Encuentre El Area Bajo La Curva De Un Diagrama PV: 5 Steps
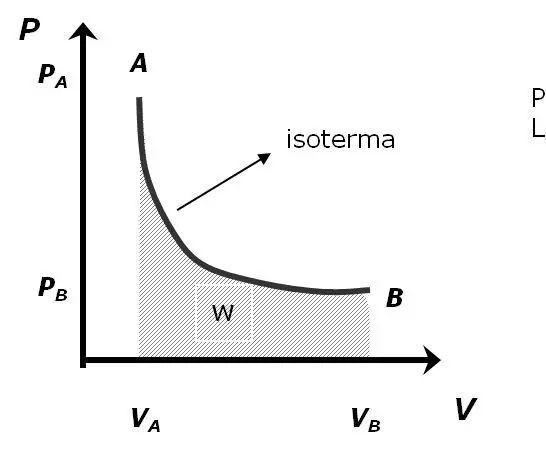
Como Crear Un Programa En Python Que Encuentre El Area Bajo La Curva De Un Diagrama PV: În acest tutorial se enes ñ ara a calcular el area low una curva cu date importate dintr-un arhiv. Pentru el se calculează zona folosind multe trapecii sumate și se colorează á el area bajo esta
Programa Python Para El Area De Un Diagrama PV: 4 Steps
Programa Python Para El Area De Un Diagrama PV: Introducucci ó n al programSe știu că el á rea sub curba unui diagrama PV determină lucrarea făcută pentru un gaz ideal. În acest program se determină lucrarea făcută pentru un gaz care se completează cu datele tomate în tabela de un
Como Hallar El Recorrido De Un Objeto Y El Área Bajo La Curva En Python: 7 Steps

Como Hallar El Recorrido De Un Objeto Y El Área Bajo La Curva En Python: Este program gr á fica la curva care există între relația ó n viteză împotriva timpului în mișcarea unui obiect. Adem á s este program calcula el recorrido that hizo este object to find the á rea debajo de la curva que
Área Bajo La Curva: 7 pași
Área Bajo La Curva: Es necesario hallar el á rea bajo la curva de una funci ó n presi ó n contra volumen pentru putere hallar el trabajo (W) que de esta, teniendo en cuenta los principios de la f í sica. Pentru a face lucrarea m á s f á cil a
Desplazarea De Un Objeto Mediante El Calculo De Área En Python: 8 Steps (with Pictures)
Desplazamiento De Un Objeto Mediante El Calculo De Área En Python: Para calcular el desplazamiento de un objeto, teniendo en cuenta los principios de la f í sica, se poate găsi el á rea de su movimiento en una gr á fica de viteză contra timpului . Sin embargo, el calculo de esta á rea n
