Simularea sistemului solar: 4 pași

2024 Autor: John Day | [email protected]. Modificat ultima dată: 2024-01-30 11:45

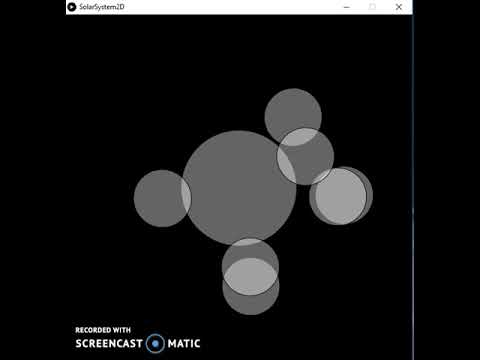
Pentru acest proiect mi-am propus să creez o simulare a modului în care gravitația afectează mișcarea corpurilor planetare într-un sistem solar. În videoclipul de mai sus \, corpul Soarelui este reprezentat de sfera cu plasă de sârmă, iar planetele sunt generate aleatoriu.

Mișcarea planetelor se bazează pe fizica reală, Legea gravitației universale. Această lege definește forța gravitațională exercitată asupra unei mase de către o altă masă; în acest caz, Soarele pe toate planetele, și planetele una pe cealaltă.

Pentru acest proiect am folosit Processing, un mediu de programare bazat pe Java. De asemenea, am folosit fișierul de exemplu Procesare care simulează gravitația planetelor. Tot ce veți avea nevoie pentru acest lucru este software-ul de procesare și un computer.

Pasul 1: Simulare 2 dimensiuni

Am început vizionând câteva videoclipuri despre cum să codificăm acest lucru pe care Dan Shiffman l-a creat pe canalul său YouTube, Coding Train (Partea 1/3). În acest moment m-am gândit că voi folosi recursivitatea pentru a genera sistemul solar, similar cu modul în care Shiffman face doar folosind legile fizicii.

Am creat un obiect de planetă care avea „planete pentru copii”, care la rândul lor aveau și planete „pentru copii”. Codul pentru simularea 2D nu a fost terminat deoarece nu am avut o modalitate excelentă de a simula forțele gravitaționale pentru fiecare planetă. Am pivotat din acest mod de gândire, într-o direcție bazată pe exemplul de procesare încorporat al atracției gravitaționale. Problema era că trebuia să calculez forța gravitațională de pe toate celelalte planete de pe fiecare planetă, dar nu mă puteam gândi cum să trag cu ușurință informațiile unei planete individuale. După ce am văzut cum o face tutorialul de procesare, mi-am dat seama exact cum să o fac folosind în schimb bucle și tablouri

Pasul 2: Luați-l la 3 dimensiuni

Folosind exemplul de cod pentru Atracția Planetară care vine odată cu procesarea, am început un nou program pentru o simulare 3D. Diferența majoră este în clasa Planet, unde am adăugat o funcție de atracție, care calculează forța gravitațională între două planete. Acest lucru mi-a permis să simulez modul în care funcționează sistemele noastre solare, unde planetele nu sunt doar atrase de soare, ci și de orice altă planetă.

Fiecare planetă are caracteristici generate aleatoriu, cum ar fi masa, raza, viteza orbitală inițială, etc. Planetele sunt sfere solide și Soarele este o sferă cu plasă de sârmă. În plus, locația camerei se rotește în jurul centrului ferestrei.

Pasul 3: Utilizarea unor planete reale

După ce am descărcat cadrul pentru simularea 3D, am folosit Wikipedia pentru a găsi datele planetei reale pentru sistemul nostru solar. Am creat o serie de obiecte planetare și am introdus datele reale. Când am făcut acest lucru, a trebuit să reduc toate caracteristicile. Când am făcut acest lucru, ar fi trebuit să iau valorile reale și să mă înmulțesc cu un factor pentru a reduce valorile, în schimb am făcut-o în unități de Pământ. Adică am luat raportul dintre valoarea Pământului și valoarea celorlalte obiecte, de exemplu, Soarele are de 109 ori mai multă masă decât Pământul. Cu toate acestea, acest lucru a dus la dimensiunile planetelor care par prea mari sau prea mici.

Pasul 4: Gânduri finale și comentarii

Dacă aș continua să lucrez la această simulare, aș rafina / îmbunătăți câteva lucruri:

1. Mai întâi aș scala totul uniform folosind același factor de scalare. Apoi, pentru a îmbunătăți vizibilitatea orbitelor, aș adăuga un traseu în spatele fiecărei planete pentru a vedea cum se compară fiecare revoluție cu precedenta

2. Camera nu este interactivă, ceea ce înseamnă că o parte din orbite sunt în afara ecranului, vizionând „în spatele persoanei”. Există o bibliotecă de camere 3D numită Peazy Cam, care este utilizată în Partea 2 a seriei video a Coding Train pe acest subiect. Această bibliotecă permite vizualizatorului să rotească, să panorameze și să zoomeze camera, astfel încât să poată urmări întreaga orbită a unei planete.

3. În cele din urmă, planetele sunt în prezent indistincte una de cealaltă. Aș dori să adaug „piei” fiecărei planete și Soare, astfel încât spectatorii să poată recunoaște Pământul și altele.