
Cuprins:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:41.
- Modificat ultima dată 2025-01-23 15:04.

acest program este de a calcula transformarea frecvenței pe arduino cu controlul bateriei asupra parametrilor.
aceasta nu este FFT
FFT este algoritmul folosit pentru a rezolva DFT cu timp mai mic.
Codul pentru FFT poate fi găsit aici.
Pasul 1: Cum funcționează (concept):


Programul dat pentru transformarea frecvenței oferă un control excelent asupra ieșirii necesare. acest program evaluează intervalul de frecvență dat de utilizator la intrarea dată pentru setul de date.
- În figură, un set de date format din două frecvențe numite f2 și f5 date care trebuie testate. f2 și f5 sunt nume aleatorii pentru două frecvențe, număr mai mare pentru frecvență relativ mai mare. aici frecvența mai mică f2 are o amplitudine mai mare și f5 are o amplitudine mai mică.
- Se poate arăta matematic că -sumarea înmulțirii a două seturi de date armonice cu frecvență diferită tinde la zero (un număr mai mare de date poate duce la rezultatul bateriei). În cazul nostru, dacă aceste două frecvențe de înmulțire au aceeași (sau foarte aproape) frecvență, suma multiplicării este un număr diferit de zero, unde amplitudinea depinde de amplitudinea datelor.
- pentru a detecta frecvența specifică, setul de date poate fi înmulțit cu diferite frecvențe de testare și rezultatul poate da componenta acelei frecvențe în date.
Pasul 2: Cum funcționează (în cod):


pentru că datele date (f2 + f5) unul câte unul f1 la f6 se înmulțește și se notează valoarea sumei. suma finală respectivă reprezintă conținutul acelei frecvențe. restul (nepotrivirea) frecvenței ar trebui să fie în mod ideal zero, dar nu este posibil în caz real. pentru a face suma zero este necesar să aveți o dimensiune infinită a seturilor de date.
- așa cum se poate arăta în figura f1 la f6 frecvența de încercare și se arată multiplicarea sa cu set de date în fiecare punct.
- în a doua figură este reprezentată însumarea acestei multiplicări la fiecare frecvență. două vârfuri la 1 și 5 sunt identificabile.
deci, folosind aceeași abordare pentru date aleatorii, putem evalua atât de multe frecvențe și analiza conținutul de frecvență al datelor.
Pasul 3: Utilizarea codului pentru analiza frecvenței:

pentru un exemplu, să folosim acest cod pentru a găsi DFT de undă pătrată.
mai întâi lipiți codul atașat (funcția DFT) după buclă așa cum se arată în imagine
8 TERMENI CARE TREBUIE SĂ FIE SPECIFICAȚI
- o matrice din care trebuie luate dft
- dimensiunea unui tablou
- interval de timp între 2 citiri în matrice în milisecunde
- valoare mai mică a frecvenței în Hz
- valoarea superioară a intervalului de frecvență în Hz
- dimensiunea treptelor pentru intervalul de frecvență
- repetarea unui semnal (minim 1) precizie mai mare a numărului de baterii, dar timp de soluție crescut
-
funcția fereastră:
0 pentru fără fereastră1 pentru fereastră plat 2 pentru fereastră hann 3 pentru fereastră cu ciocan
(dacă nu aveți nicio idee despre selectarea ferestrei păstrați implicit 3)
exemplu: dft (a, 8, 0,5, 0, 30, 0,5, 10, 3); aici a este o matrice de element de dimensiunea 8 care trebuie verificată pentru 0 Hz până la 30 Hz cu 0,5 trepte (0, 0,5, 1, 1,5, …, 29, 29,5, 30) 10 fereastră de repetare și ciocănire
aici este posibil să se utilizeze o matrice de dimensiuni mai mari cât poate suporta arduino.
Pasul 4: ieșire:


dacă comentați
Serial.print (f); Serial.print ("\ t");
din cod, serialul plotter va da natura spectrului de frecvență, dacă nu, monitorul serial ar da frecvență cu amplitudinea sa.
Pasul 5: Verificarea diferitelor dimensiuni ale ferestrei și eșantionului:

în figură, frecvența undei sinusoidale este măsurată folosind diferite setări.
Pasul 6: Exemplu:

în comparație cu transformarea datelor folosind SciLab și arduino.
Recomandat:
Transformarea camerei tale într-un Mars Rover: 5 pași

Transformându-ți Roomba într-un Mars Rover:
Filtrare FIR pentru detectarea mai frecventă a frecvenței: 5 pași
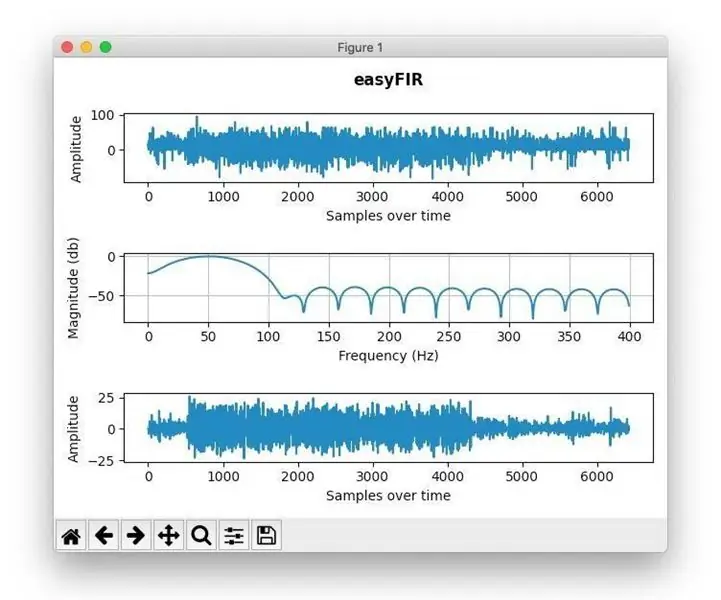
Filtrare FIR pentru o detecție mai frecventă a frecvenței: Sunt un mare fan al instruirii lui akellyirl despre detectarea frecvenței fiabile folosind tehnici DSP, dar uneori tehnica pe care a folosit-o nu este suficient de bună dacă aveți măsurători zgomotoase. frecvență det
Măsurarea frecvenței și tensiunii de alimentare cu ajutorul Arduino: 6 pași

Măsurarea frecvenței și tensiunii de alimentare folosind Arduino: Introducere: Scopul acestui proiect este de a măsura frecvența și tensiunea de alimentare, care este cuprinsă între 220 și 240 Volți și 50Hz aici în India. Am folosit un Arduino pentru captarea semnalului și calcularea frecvenței și tensiunii, puteți utiliza orice alt microcont
Temporizator Circuit 555 de blocare a frecvenței radio: 6 pași

Temporizator 555 al circuitului de blocare a frecvenței radio: un circuit de blocare a frecvenței radio (RF) este auto-explicativ în ceea ce face. Este un dispozitiv care interferează cu recepția semnalelor RF ale anumitor electronice care utilizează frecvențe similare și se află în apropierea jammerului. Acest circuit de jammer
Transformarea difuzoarelor audio: DIY (Made in Fusion 360): 18 pași (cu imagini)

Transformarea difuzoarelor audio: DIY (Made in Fusion 360): Am o pereche de difuzoare pe care le-am realizat acum 2 ½ ani. Dar cutiile vorbitorului sunt neorganizate și folosesc mult spațiu. Prin urmare, aș dori să-mi refac difuzorul audio făcând cutia sau carcasa în imprimarea 3D. Difuzorul este bun doar pentru computer
