
Cuprins:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:41.
- Modificat ultima dată 2025-01-23 15:04.


Iată o aplicație practică a ecuațiilor matematice complexe.
Aceasta este de fapt o tehnică foarte utilă pe care o puteți utiliza pentru a caracteriza componentele, sau chiar o antenă, la frecvențe prestabilite.
Dacă ați făcut jocuri cu electronica, este posibil să fiți familiarizați cu rezistențele și legea lui Ohm. R = V / I S-ar putea să fiți surprins acum să știți că este tot ce trebuie să rezolvați și pentru impedanța complexă! Toate impedanțele sunt în esență complexe, adică au o parte reală și o parte imaginară. În cazul unui rezistor imaginarul (sau reactanța) este 0, în mod corespunzător nu există o diferență de fază între V și I, deci le putem lăsa afară.
Un rezumat rapid al numerelor complexe. Complex înseamnă pur și simplu că numărul este format din două părți, una reală și una imaginară. Există două moduri de a reprezenta numere complexe, de exemplu în figura de mai sus, un punct ar putea fi definit de valorile reale și imaginare, cum ar fi unde se întâlnesc liniile galbene și albastre. De exemplu, dacă linia albastră ar fi la 4 pe axa X și 3 pe axa Y, acest număr ar fi 4 + 3i, i indică faptul că aceasta este partea imaginară a acestui număr. O altă modalitate de a defini același punct ar fi prin lungimea (sau amplitudinea) liniei roșii, precum și ce unghi face cu orizontală. În exemplul de mai sus, aceasta ar fi 5 <36,87.
Sau o linie cu o lungime de 5 la un unghi de 36,87 grade.
În ecuația de deasupra tuturor parametrilor, R, V și I pot fi considerați ca având o parte imaginară, atunci când lucrați cu rezistențe, această valoare este 0.
Când lucrați cu inductoare sau condensatoare sau când se poate măsura o diferență de fază (în grade) între semnale, ecuația rămâne aceeași, dar trebuie inclusă partea imaginară a numărului. Majoritatea calculatoarelor științifice facilitează lucrul cu matematica complexă, în acest tutorial voi lucra printr-un exemplu pe un Casio fx-9750GII.
În primul rând, o recapitulare a ecuației divizorului de tensiune a rezistorului.
Conform cifrei -
Tensiunea la Y este curentul i înmulțit cu R2
i este tensiunea X împărțită la suma lui R1 și R2
Când R2 este necunoscut, putem măsura celelalte valori, X, Y, R1 și aranjăm din nou ecuația pentru a rezolva pentru R2.
Provizii
Calculator stiintific
Generator de semnal
Osciloscop
Pasul 1: Configurare

Să presupunem că vrem să calculăm inductanța dispozitivului sub test (DUT) la 1 MHz.
Generatorul de semnal este configurat pentru o ieșire sinusoidală de 5V la 1MHZ.
Folosim rezistențe de 2k ohm, iar canalele osciloscopului sunt CH1 și CH2
Pasul 2: Osciloscop

Obținem formele de undă așa cum se arată în figură. O schimbare de fază poate fi văzută și măsurată pe osciloscop, conducând cu 130ns. Amplitudinea este de 3,4V. Notă, semnalul de pe CH1 ar trebui să fie de 2,5V, deoarece este luat la ieșirea divizorului de tensiune, aici este prezentat ca 5V pentru claritate, deoarece aceasta este valoarea pe care trebuie să o folosim și în calculele noastre. adică 5V este tensiunea de intrare către divizorul cu componenta necunoscută.
Pasul 3: Calculați faza

La 1 MHz perioada semnalului de intrare este 1us.
130ns oferă un raport de 0,13. Sau 13%. 13% din 360 este 46,6
Semnalului de 5V i se dă un unghi de 0.. deoarece acesta este semnalul nostru de intrare și schimbarea de fază este relativă la acesta.
semnalului de 3,4V i se dă unghiul de +46,6 (+ înseamnă că conduce, pentru un condensator unghiul ar fi negativ).
Pasul 4: pe Calculator


Acum pur și simplu introducem valorile măsurate în calculator.
R este 2k
V este 5 (EDIT - V este 5, mai târziu în ecuație se folosește X! Rezultatul este exact același cu i are X ca 5 în calculatorul meu)
Y este tensiunea noastră măsurată cu unghiul de fază, acest număr este introdus ca un număr complex, pur și simplu specificând unghiul așa cum se arată pe ecranul calculatorului
Pasul 5: Rezolvați ecuația

acum ecuația
(Y * R) / (X - Y)
este introdus în calculator, aceasta este exact aceeași ecuație pe care o folosim pentru a rezolva divizoarele de tensiune ale rezistorului:)
Pasul 6: valori calculate


Calculatorul a dat rezultatul
18 + 1872i
18, este partea reală a impedanței și are o inductanță de +1872 la 1MHz.
Care funcționează la 298uH conform ecuației impedanței inductorului.
18 ohmi este mai mare decât rezistența care ar fi măsurată cu un multimetru, deoarece multimetrul măsoară rezistența la curent continuu. La 1 MHz există efect de piele, în care partea interioară a conductorului este ocolită de curent și curge doar în exteriorul cuprului, scăzând efectiv zona transversală a conductorului și sporind rezistența acestuia.
Recomandat:
DIY Cum să controlați unghiul motorului servo utilizând componenta secvenței Visuino: 10 pași

DIY Cum se controlează unghiul servomotorului utilizând componenta de secvență Visuino: În acest tutorial vom folosi Servo Motor și Arduino UNO și Visuino pentru a controla unghiul servomotorului utilizând componenta secvenței. Componenta secvenței este perfectă pentru situațiile în care dorim să declanșăm mai multe evenimente în ordine. în cazul nostru servo motor degr
Cum să alegeți amprenta componentă corectă: 3 pași
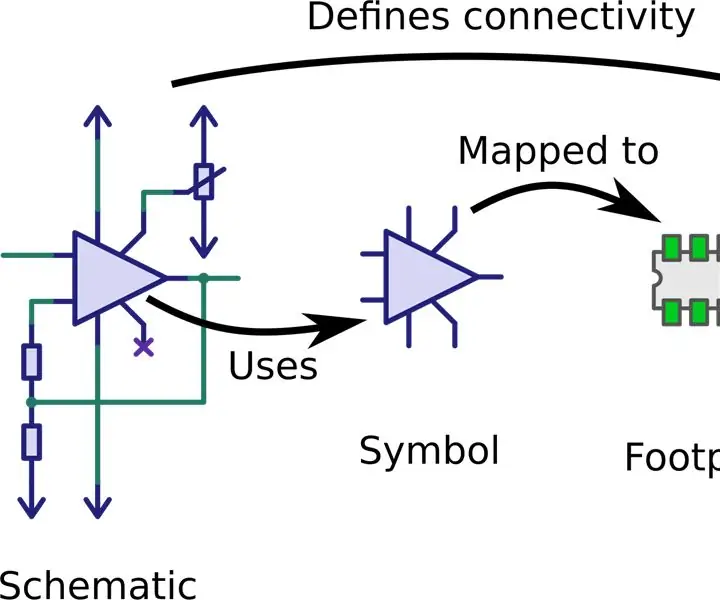
Cum să alegeți amprenta corectă a componentelor: o amprentă sau un model terestru este aranjarea plăcuțelor (în tehnologia de montare la suprafață) sau a orificiilor de trecere (în tehnologia prin găuri) utilizate pentru atașarea fizică și conectarea electrică a unei componente la o placă de circuite imprimate . Modelul terenului pe un circuit
Circuitul de blocare cu UC. Un singur buton. Un Pin. Componentă discretă .: 5 pași

Circuitul de blocare cu UC. Un singur buton. Un Pin. Componentă discretă: Bună ziua tuturor, căutam un circuit de pornire / oprire pe net. Tot ce am găsit nu a fost ceea ce căutam. Vorbeam cu mine, există neapărat o cale spre asta. De asta aveam nevoie.-Doar un singur buton de apăsat pentru a activa sau dezactiva.-Trebuie să folosesc doar
Partea 1. ThinkBioT Autonome senzor bioacustic Componenta hardware: 13 pași

Partea 1. ThinkBioT Autonome senzor bioacustic Construire hardware: ThinkBioT își propune să ofere un cadru software și hardware, conceput ca o coloană vertebrală tehnologică pentru a sprijini cercetările ulterioare, gestionând detaliile de colectare a datelor, pre-procesare, transmisie de date și sarcini de vizualizare care să permită cercetător
Cum să lipiți o componentă prin gaură: 8 pași

Cum să lipiți o componentă prin găurire: există două tipuri principale de componente găurite prin care vom trece în acest „Cum să lipiți” ghidaj, componente cu orificiu axial cu plumb și pachete duale în linie (DIP ’ s). Dacă ai făcut un pic de breadboarding, tu
