Cum să creați o cupolă geodezică în stil Temcor în Autodesk Inventor: 8 pași

2024 Autor: John Day | [email protected]. Modificat ultima dată: 2024-01-30 11:45

Acest tutorial vă va arăta cum să creați o cupolă în stil Temcor folosind doar puțină matematică.

Majoritatea informațiilor din acest tutorial au fost extrase din tehnica inversă a TaffGoch a metodei de subdiviziune a vechii stații Amundsen-Scott South Pole Station, deci o mulțumire imensă lui!

Un avantaj major al domurilor Temcor este numărul lor scăzut unic de strut - crește aritmetic cu frecvența, nu spre deosebire de rețeaua geodezică triacontahedră regulată a lui Duncan Stuart (Metoda 3 *), dar rezultatul pare mult mai plăcut.

Pentru simplitate, frecvența cupolei pe care o realizăm este de 14, astfel încât factorii acordului pot fi contrastați cu modelul Temcor al lui TaffGoch.

Inventorul 2016.ipt este inclus la sfârșitul tutorialului.

*ACTUALIZAȚI*

Am descris Metoda 4 ca rețeaua geodezică triacontahedră regulată a lui Duncan Stuart, dar nu este. Metoda a fost de fapt inventată de Christopher Kitrick, care, în lucrarea sa din 1985, „Geodesic Domes”, a descris construcția acesteia. În plus, în lucrarea sa din 1990, „A Unified Approach to Class I, II & III Geodesic Domes”, el prezintă alte 8 metode, una dintre ele fiind Metoda 3 a lui Duncan Stuart, cealaltă propria „Metodă 4” și, surprinzător suficient, o metodă similară cu cea a lui Temcor, pe care o numește „Metoda aa” (Pasul 7 arată cum Temcor a modificat „Metoda aa”). Într-un viitor instructiv, voi descrie construcția metodelor prezentate în această din urmă lucrare.

Pasul 1: Parametrii utilizatorului

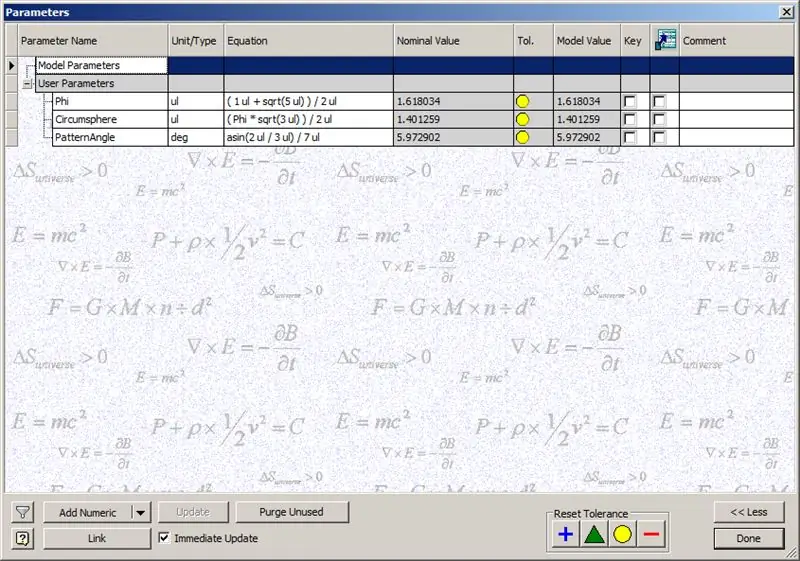
Înainte de a începe construirea cupolei, introduceți parametrii afișați:

Phi - Raportul de aur. Definit ca ((1 + √5 /) 2

Circumsphere - Aceasta este circumfera unui dodecaedru, definit ca ((Phi * √3) / 2)

PatternAngle - Acesta este unghiul central al unui dodecaedru. Deoarece frecvența cupolei noastre este 14, împărțim acest unghi central la jumătate din frecvență, în acest caz, 7.

Pasul 2: Schițarea unui dreptunghi auriu

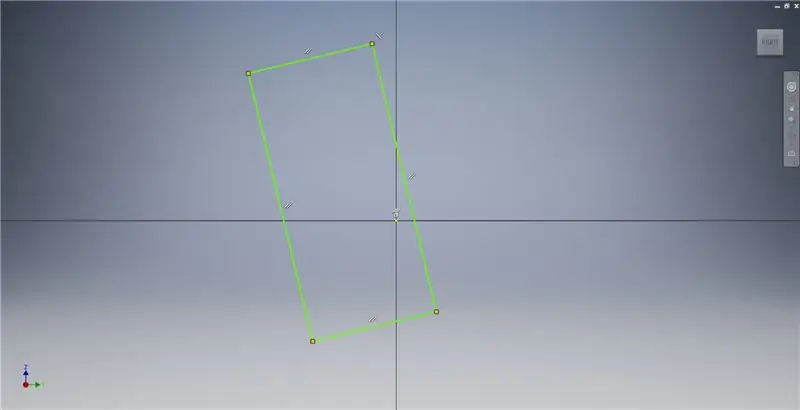
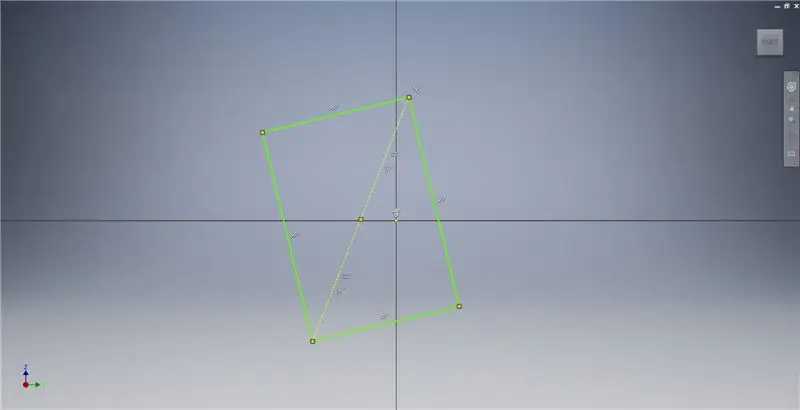
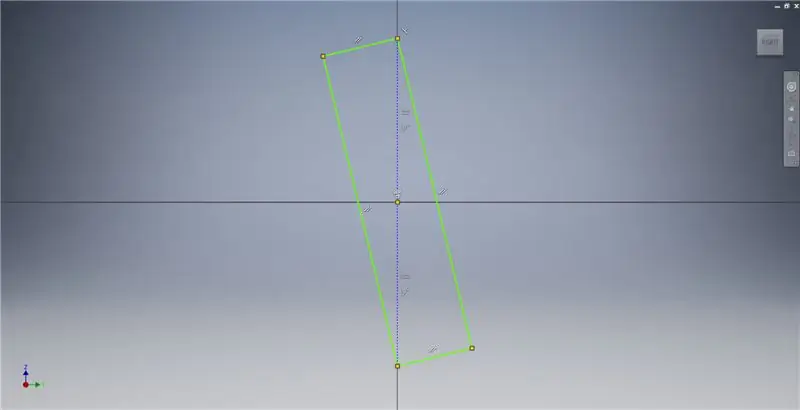
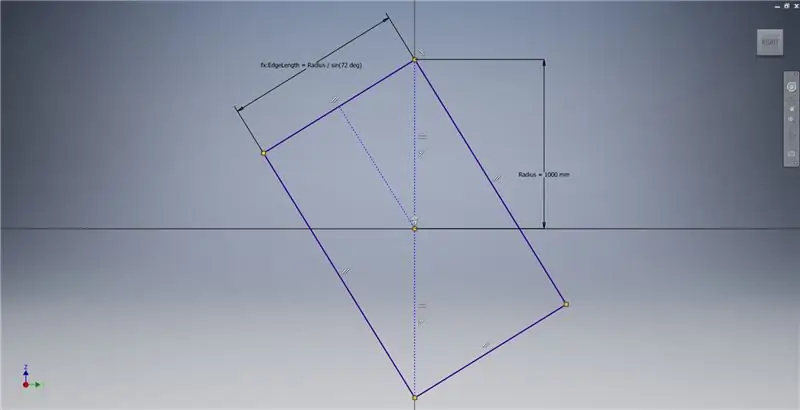
Porniți o schiță pe planul YZ, apoi creați un dreptunghi cu trei puncte așa cum se arată, referindu-vă la notele de imagine pentru informații suplimentare care descriu crearea unui dreptunghi de aur.

Pasul 3: Crearea unui dreptunghi Golden²

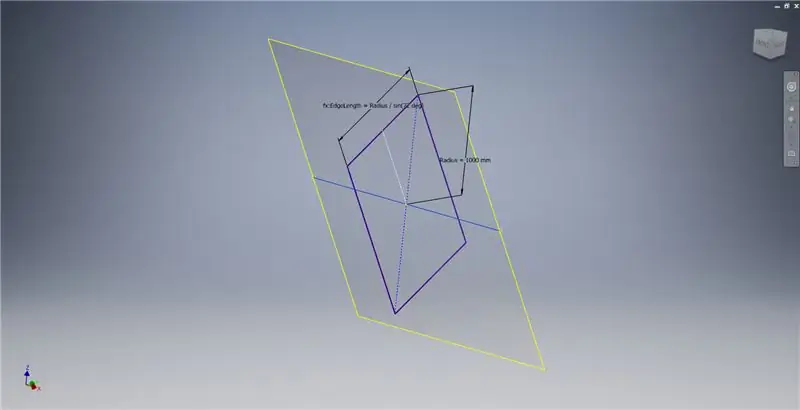
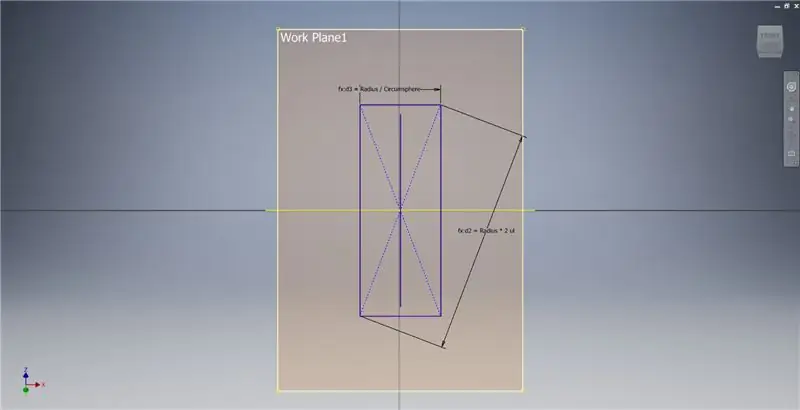
Creați un plan de lucru folosind axa X și linia evidențiată în prima imagine, apoi începeți o altă schiță pe acest plan de lucru. Construiți un dreptunghi punct central începând de la origine, apoi dimensionați dreptunghiul așa cum se arată în a treia imagine.

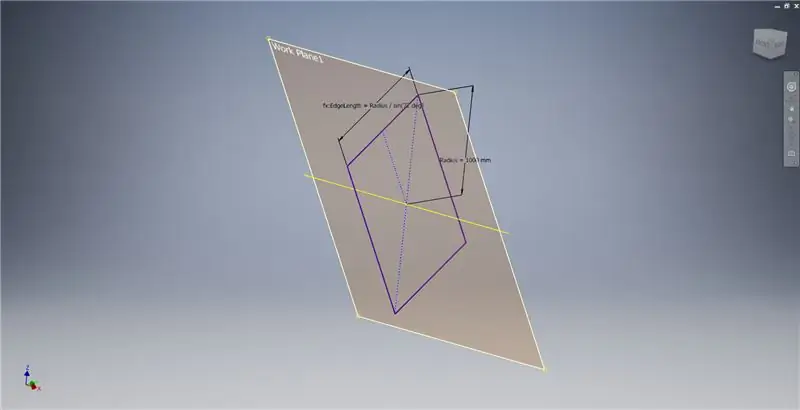
Pasul 4: Crearea triunghiului Triacon 2v

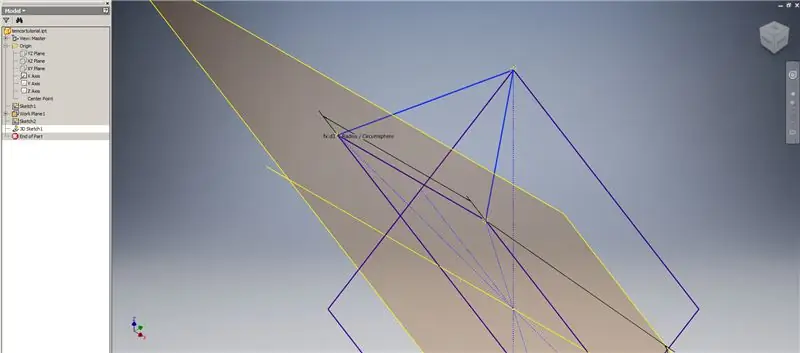
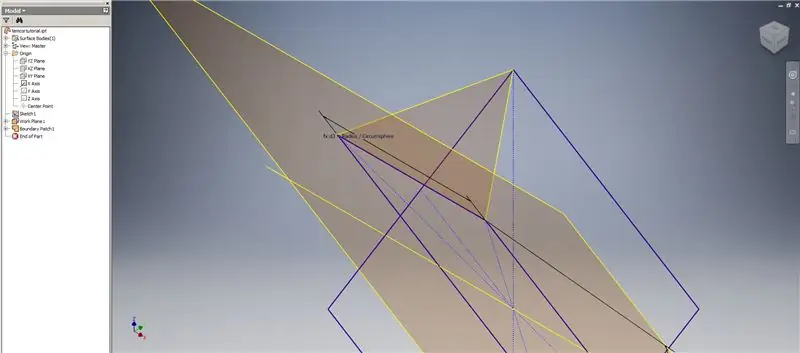
Acum, că avem toată geometria de care avem nevoie, formați patch-ul de graniță în a doua imagine folosind orice metodă preferați. Am ales să fac o schiță 3D, dar schițarea pe un alt plan de lucru ar funcționa la fel de bine.

Pasul 5: Crearea planurilor de intersecție

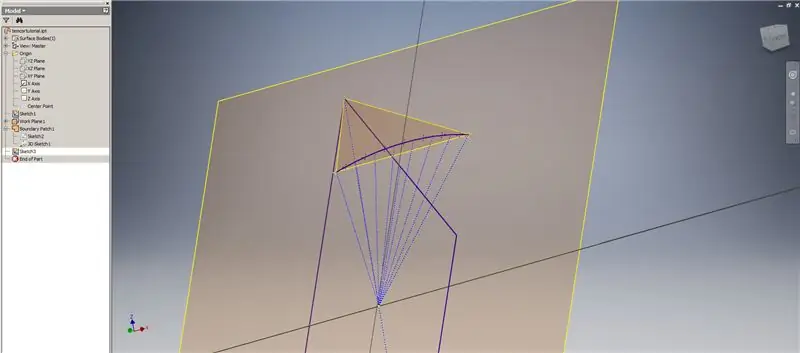
Începeți o altă schiță pe primul plan de lucru („Planul de lucru 1”) pe care l-ați creat, proiectați colțurile dreptunghiului Golden², apoi conectați aceste puncte și originea pentru a forma unghiul central al triacontahedronului de 2v. Împărțiți-l la jumătate din frecvența cupolei, ca și când ați începe o defecțiune a Metodei 2. Plasați puncte pe punctele medii ale acordurilor.

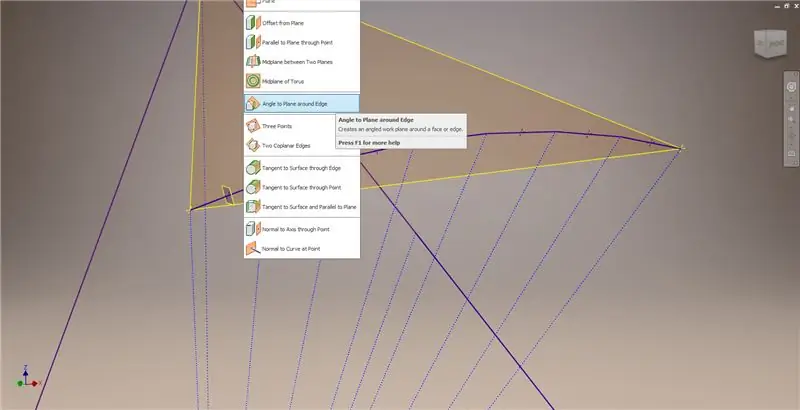
Ieșiți din schiță, apoi creați un plan folosind unul dintre acorduri și punctul de mijloc al acestuia, așa cum se arată în a doua imagine. Apoi, creați un alt plan de lucru folosind „Unghi la plan în jurul muchiei”. Selectați Planul de lucru 1 și una dintre liniile de construcție afișate în imaginea din dreapta și din stânga jos. Acceptați unghiul implicit de 90 de grade, altfel restul subdiviziunii nu ar arăta corect. Repetați procesul folosind restul acordurilor și liniilor de construcție pentru a obține rezultatul în imaginea din dreapta jos.

Pasul 6: Crearea curbelor de intersecție și formarea subdiviziunii

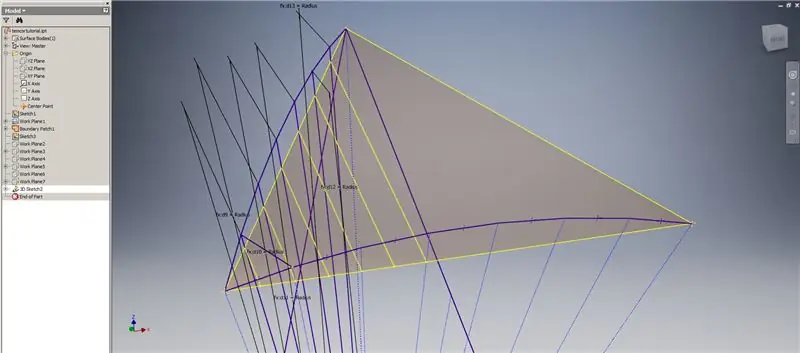
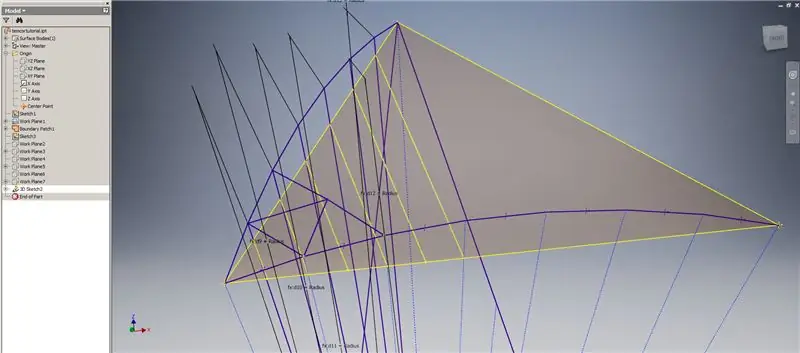
Porniți o schiță 3D, apoi creați curbe de intersecție folosind planurile de lucru pe care tocmai le-ați creat și patch-ul de graniță, formând liniile afișate în imaginea de sus.

Desenați linii coincidente cu punctele finale ale curbelor de intersecție așa cum se arată în imaginea 2. Faceți-le pe toate egale cu raza cupolei. Desenați acordurile care unesc liniile care se află pe curbele de intersecție. Conectați orice geometrie care arată suficient de aproape pentru a forma un triunghi al subdiviziunii. Consultați următoarele 10 imagini pentru care acordurile să fie oglindite de-a lungul planurilor de lucru de intersecție - o pot explica mai bine decât o pot face doar cuvintele.

Pasul 7: Finalizarea domului

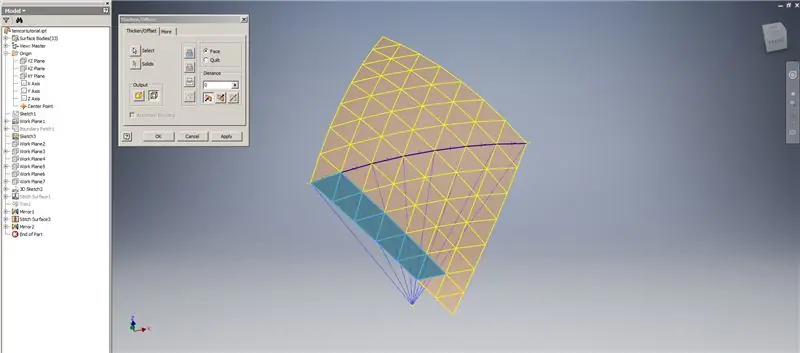
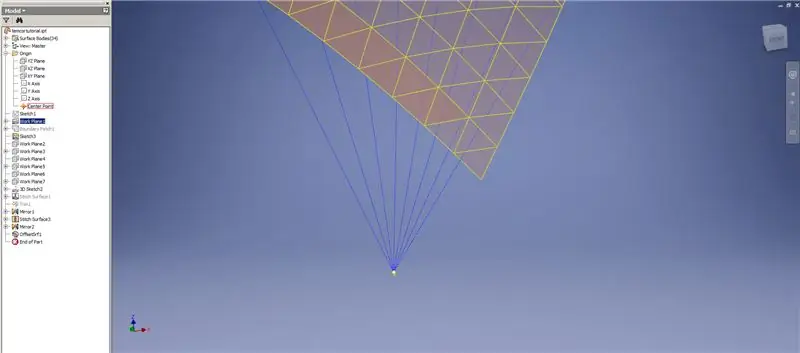
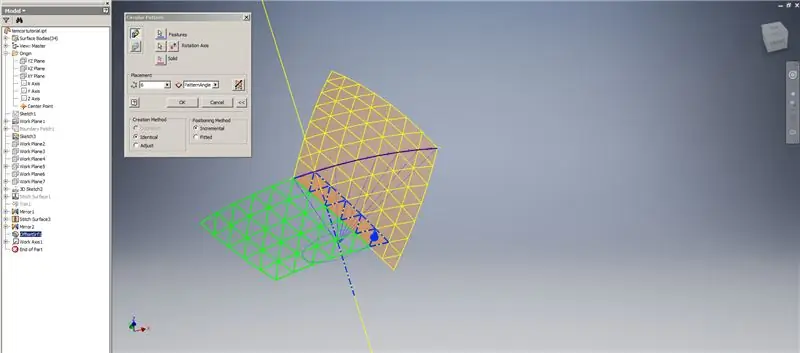
Creați un Thicken / Offset al rândurilor de jos, omițând ultimele două rânduri de triunghiuri. Modelați noul OffsetSrf de 6 ori sau ((Frecvență = 14) / 2) -1. Ascundeți OffsetSrf, coaseți suprafețele modelate, apoi oglindiți suprafața cusută cu planul YZ. Creați planuri de lucru așezate pe vârfurile triunghiului superior, așa cum se arată în imaginea 6. Tăiați suprafețele cusute și oglindite folosind aceste noi planuri de lucru, apoi cusăturați suprafețele rămase. Modelați această ultimă suprafață pe axa Z, apoi îmbinați aceste suprafețe finale și ați terminat!

Pasul 8: Verificarea acordurilor

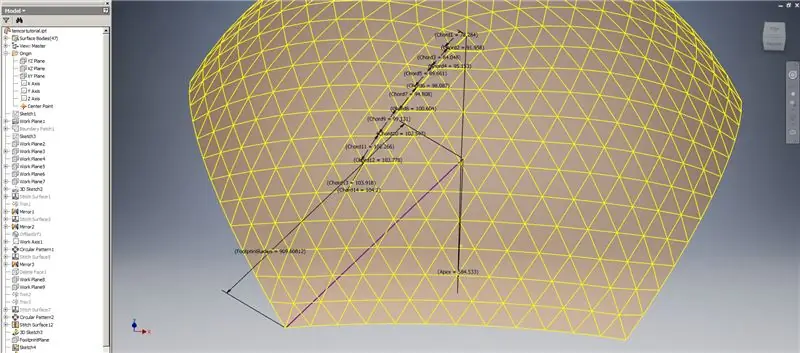
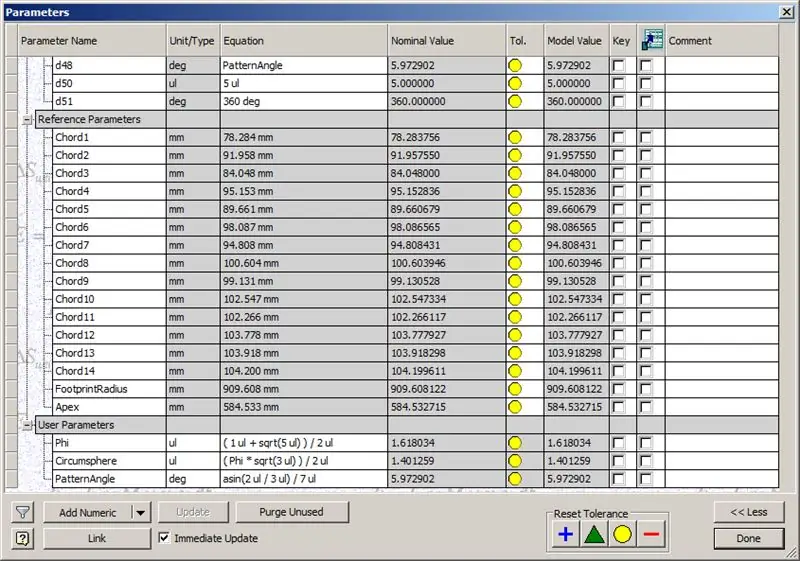
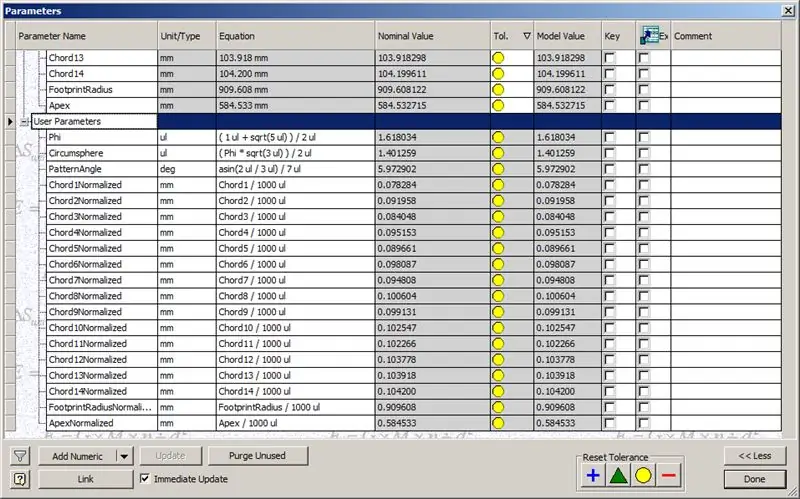
Deci, cupola noastră este terminată, dar să vedem dacă numerele se potrivesc cu modelul lui TaffGoch:

Urmând parametrii de referință, se pare că se potrivesc perfect!

Împărțind lungimile coardei la 1000, putem vedea clar o corespondență perfectă cu factorii de coardă ai modelului TaffGoch, precum și cu raza amprentei și factorii apex.