Știți despre ajustarea ESP32 ADC ?: 29 de pași

2024 Autor: John Day | [email protected]. Modificat ultima dată: 2024-01-30 11:44

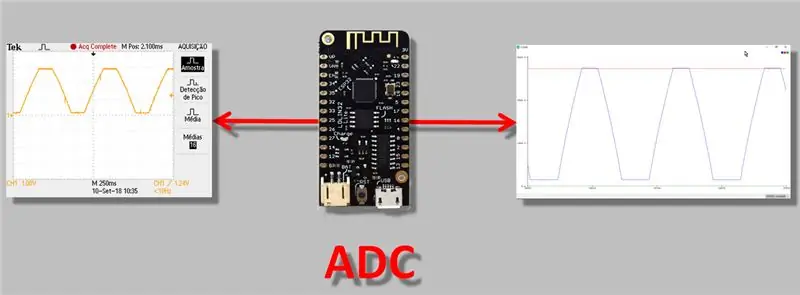
Astăzi, voi vorbi despre o problemă mai tehnică, dar una cred că toți cei care lucrează cu ESP32 ar trebui să știe: problema ADC (convertor analog-digital) reglează citirea. Mi se pare important acest lucru pentru că atunci când faci o „măsurare”, în special cu un instrument care are o ieșire analogică, trebuie să fii absolut sigur că citirea este efectuată corect.

Prin urmare, în videoclipul de astăzi vom efectua măsurători folosind „convertorul analog-digital” al ESP32, vom observa discrepanțele de conversie și vom aplica o metodă de ajustare / calibrare ADC.

Pasul 1: Ce este un convertor AD?

Un convertor AD este un circuit capabil să traducă o cantitate analogică (continuă) în valori digitale (discrete). Ce înseamnă asta? Înseamnă că, în timp ce valorile digitale pot presupune doar valori discrete formate prin combinația de zerouri și unele, o cantitate analogică poate asuma orice valoare într-un interval. De exemplu, dacă am măsura tensiunea unei celule AA ideale, am putea găsi orice valoare între 0V și 1,5V, deoarece aceasta este o cantitate analogică. Starea de ieșire a unei lămpi ideale trebuie să presupună doar două stări (oprită sau aprinsă), care este o magnitudine discretă. Deoarece microcontrolerele funcționează folosind această logică discretă, avem nevoie de un circuit capabil să traducă o cantitate analogică în digital (sau discret).

Pasul 2: Resurse utilizate

• Un card Lolin32 Lite v1.0.0

• Un osciloscop Tektronix TDS1001C pentru captare

• Un cablu USB pentru ESP32

• Un osciloscop Hantek DSO4102C ca generator de semnal

Pasul 3: ESP32 ADC

Conform datelor Espressif, cipurile ESP32 pot prezenta o diferență de +/- 6% de la un cip la altul în rezultatele măsurate.

În plus, conversia NU are un răspuns liniar pentru fiecare interval disponibil pentru citire. Espressif oferă o metodă de calibrare și sugerează utilizatorilor să implementeze alte metode dacă consideră că este necesar să se obțină acuratețea dorită.

Vom efectua o achiziție de date și, din aceasta, vom arăta răspunsurile ADC și un exemplu de aplicare a unui proces matematic pentru a citi ajustarea.

Există mai multe modalități (mai simple sau mai complexe) de a realiza aceste remedieri. Depinde de dvs. să evaluați cel mai potrivit pentru proiectul dvs.

Cel prezentat aici va avea un scop ilustrativ și va încerca să abordeze puncte interesante care pot fi observate în timpul ajustărilor.

Pasul 4: Circuit utilizat

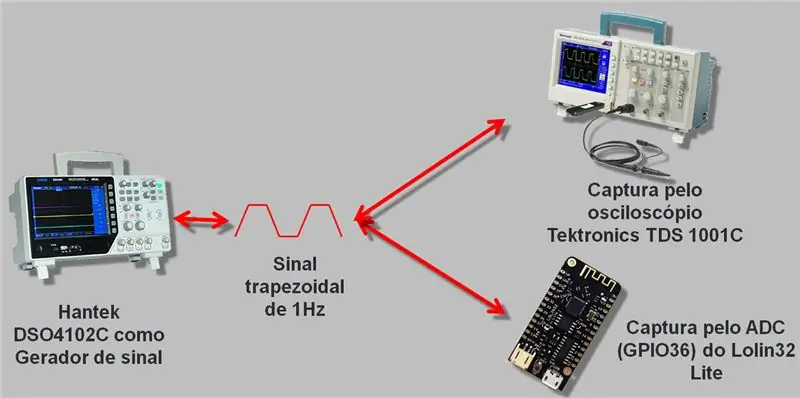
Am folosit un osciloscop cu un generator de semnal care urcă până la 25 MHz, Hantek DSO4102C. Am generat o undă care a fost citită de ESP A / D și de osciloscop. Datele colectate au fost înregistrate în CSV și într-o foaie de calcul, pe care o voi lăsa la sfârșitul articolului pentru descărcare.

Pasul 5: Semnul folosit

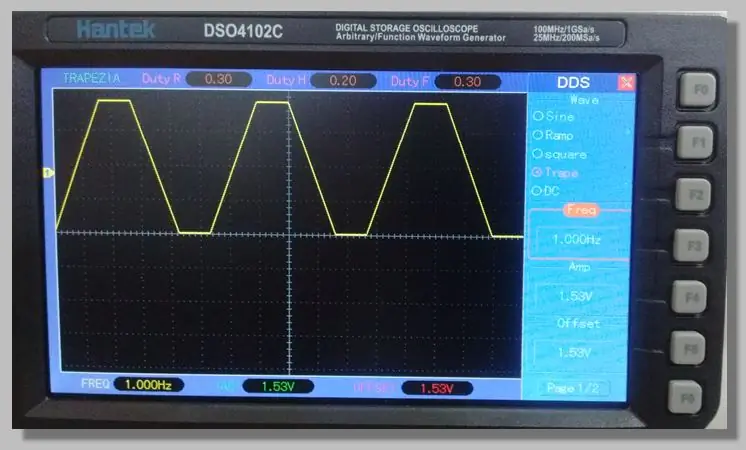
Am ales un semnal trapezoidal de joasă frecvență care permite accesul la rampele care traversează întregul interval de conversie. Acest lucru permite un număr mare de probe pe aceste rampe.

Pasul 6: Date obținute de osciloscop

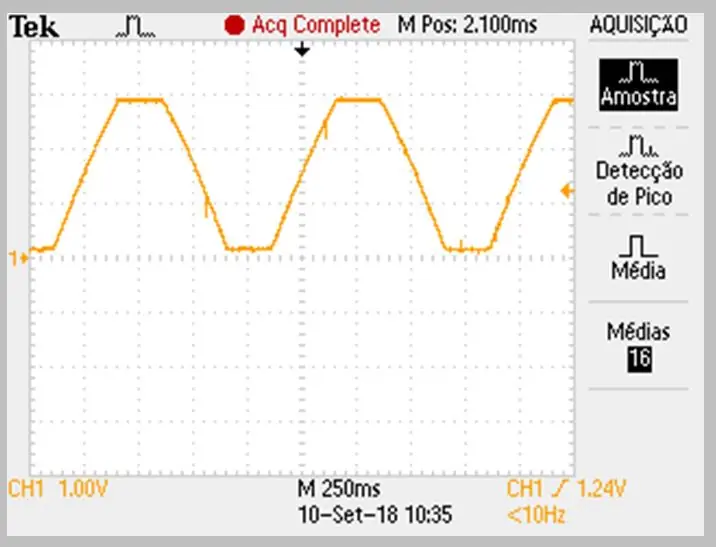
Imaginea capturii a fost realizată de osciloscop. Datele au fost stocate într-un fișier CSV. Rețineți ușoara curbură pe rampele de creștere și de coborâre ale semnalului.

Pasul 7: Date obținute de osciloscop (fișier CSV în Excel)

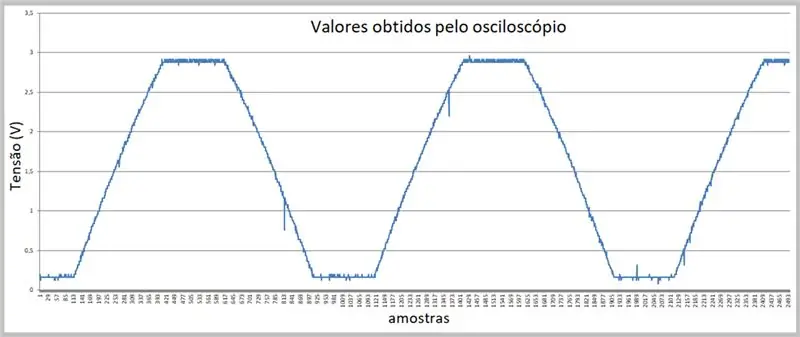
Avem probele aici.

Pasul 8: Date obținute de ADC

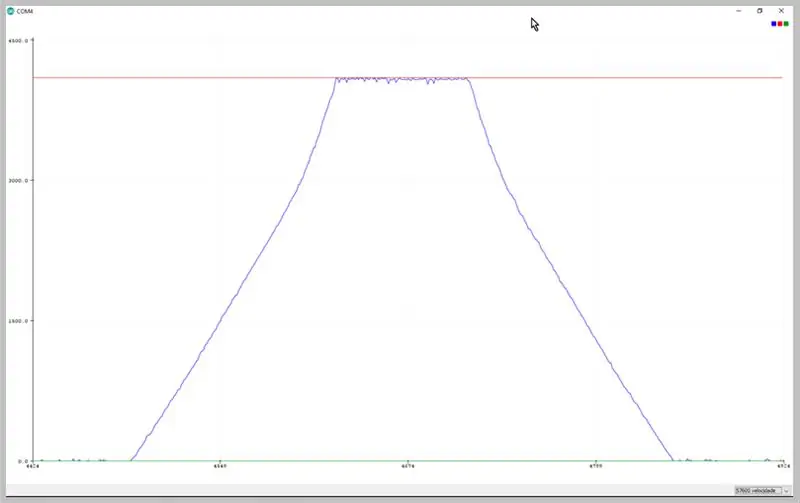
Modificând rata de transfer a serialului, putem vizualiza datele captate de ADC. Observați deformarea semnalului trapezoidal.

Date observate pe plotterul serial Arduino IDE

Pasul 9: Date obținute de ADC - Excel

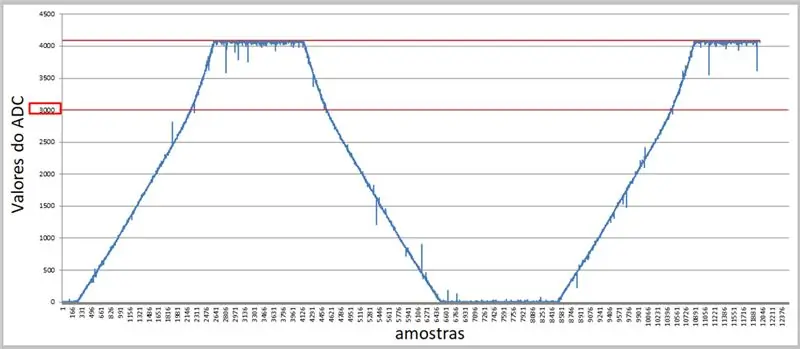
Folosind o rată mai mare și terminalul serial, putem capta valorile și le putem aplica în Excel pentru comparațiile noastre.

Pasul 10: Compararea rampelor de urcare

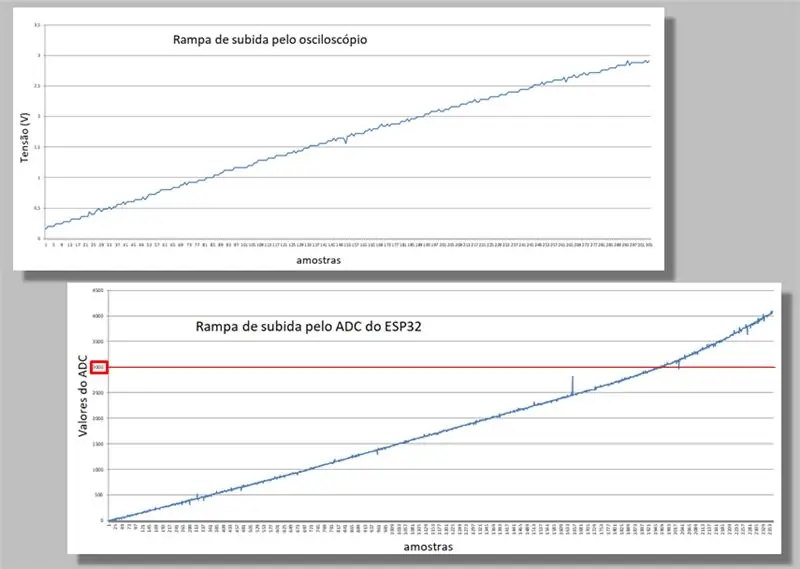
Comparăm cele două rampe de urcare ale celor două capturi.

Rețineți curbura care apare pe ambele rampe.

Rețineți, de asemenea, că pentru aceeași rampă, avem multe mai multe mostre de ESP32 decât de la osciloscop.

Pasul 11: Echivalarea numărului de probe

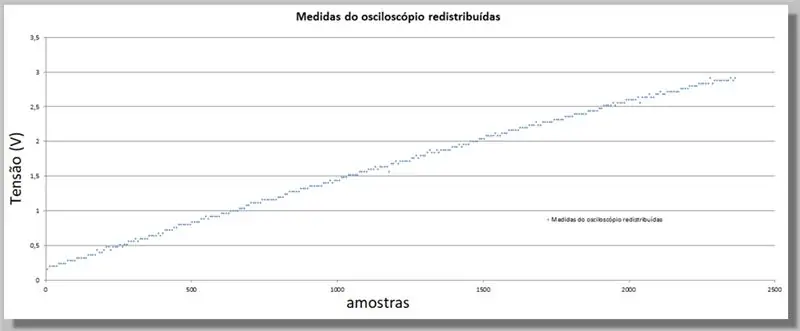
Deoarece ESP32 a furnizat un număr mai mare de probe decât osciloscopul, trebuie să echivalăm aceste valori, deoarece acestea vor servi drept indice pentru a compara cele două curbe.

Pentru aceasta, vom face o comparație directă.

Avem 305 probe pentru rampa osciloscopului și 2365 probe pentru rampa ADC.

Deoarece rampele sunt de aceeași gamă, putem spune că avem aproximativ 7,75 mostre de ADC pentru fiecare osciloscop.

Înmulțirea indicelui fiecărei probe de osciloscop are aceeași curbă, dar cu indici echivalenți cu ADC și cu datele redistribuite.

Pentru a completa datele lipsă pentru noile poziții, vom aplica o curbă care se potrivește statistic cu datele cunoscute.

Pasul 12: Umplerea golurilor - Linia de tendință

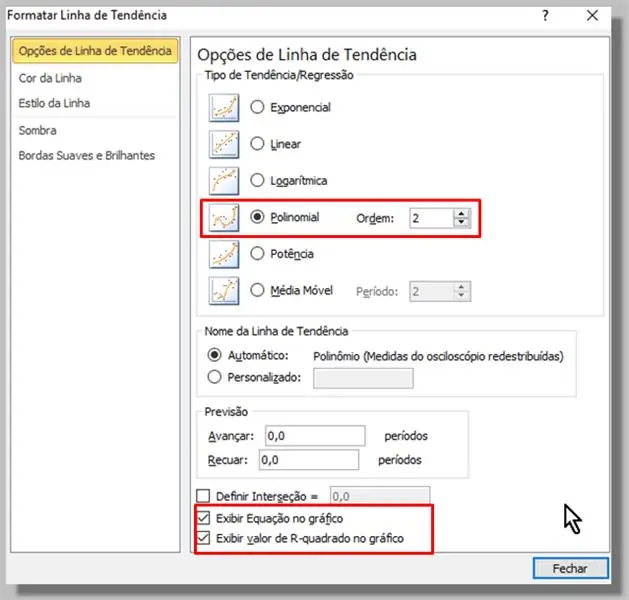
Selectând datele cunoscute (puncte albastre), făcând clic și apoi făcând clic cu butonul din dreapta, selectăm: „Adăugați linie de tendință …”

În fereastra care apare, selectăm tipul Polinom (ordinea 2 va fi suficientă).

De asemenea, am bifat opțiunile „Vizualizați ecuația în grafic” și „Afișați valoarea pătrată R în grafic”.

Facem clic pe „Închide”.

Pasul 13: Completarea golurilor - Curba polinomială de gradul 2

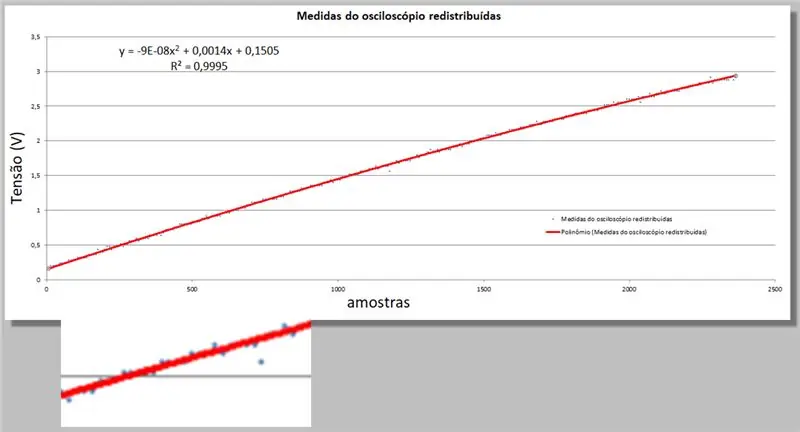
Excel ne oferă două informații noi; ecuația de ordinul doi care se potrivește cel mai bine datelor și ecuația R-pătrat care cuantifică această adecvare.

Amintiți-vă doar că, cu cât este mai aproape de 1, cu atât este mai adecvată ecuația.

Să nu aprofundăm matematica implicată, să o folosim doar ca instrument.

Pasul 14: Completarea golurilor - Evaluarea funcției

Să completăm golurile de eșantionare cu datele generate de ecuație. Și apoi, compară-le punct cu punct.

y = -9E-08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Tensiunea osciloscopului = -9E-08 * index2 + 0, 0014 * index + 0, 1505

Pasul 15: Conversia tensiunii osciloscopului la o valoare echivalentă de comparat cu ADC

Să profităm de acest lucru pentru a transforma, de asemenea, valoarea tensiunii osciloscopului într-o valoare ADC echivalentă.

Deoarece cea mai mare valoare obținută în ADP-ul ESP32 a fost 4095, ceea ce echivalează cu citirea a 2.958V pentru același indice, putem spune că:

Fiecare volt din măsurătorile osciloscopului este egal cu aproximativ 1384,4 unități ale AD. Prin urmare, putem înmulți toate măsurătorile osciloscopului cu această valoare.

Pasul 16: Compararea celor două rampe obținute

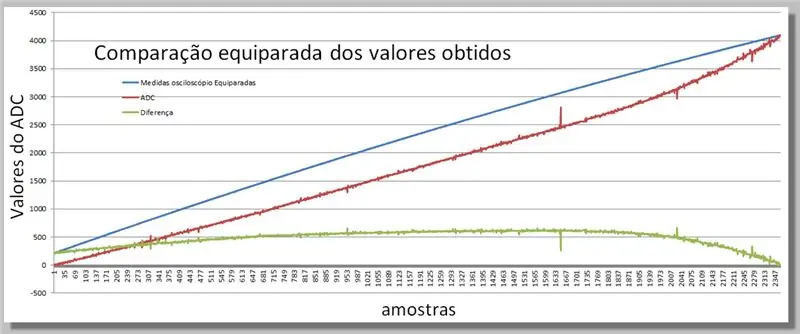
Vizualizarea diferențelor obținute în cele două lecturi.

Pasul 17: Comportamentul diferenței de citire ADC (ERROR)

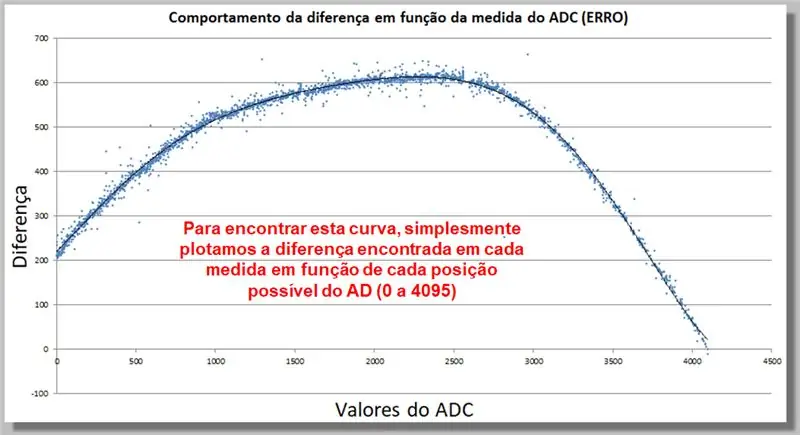
Curba de mai jos arată cum se comportă diferența în citirea ADC în funcție de măsurare. Această colectare de date ne va permite să găsim o funcție de corecție.

Pentru a găsi această curbă, reprezentăm pur și simplu diferența găsită în fiecare măsură în funcție de fiecare poziție AD posibilă (0 la 4095).

Pasul 18: Comportamentul diferenței de citire ADC - Găsirea unei funcții de corecție

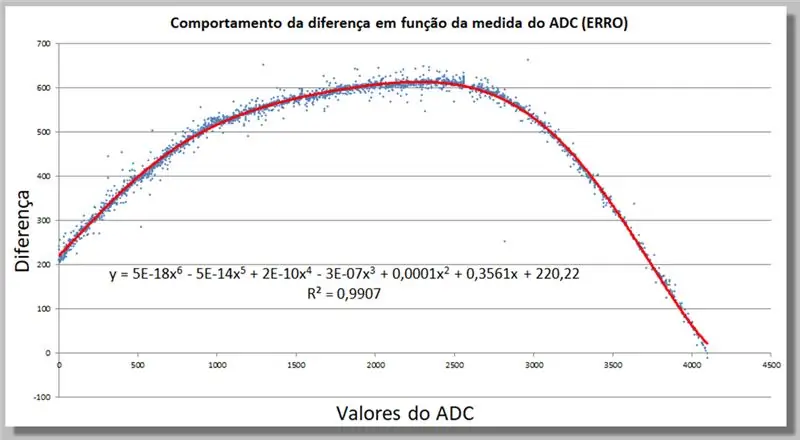
Putem determina în Excel o funcție de corecție prin adăugarea unei linii de trend, acum de un grad mai înalt, până când se potrivește suficient cu datele noastre.

Pasul 19: Utilizarea altor programe software

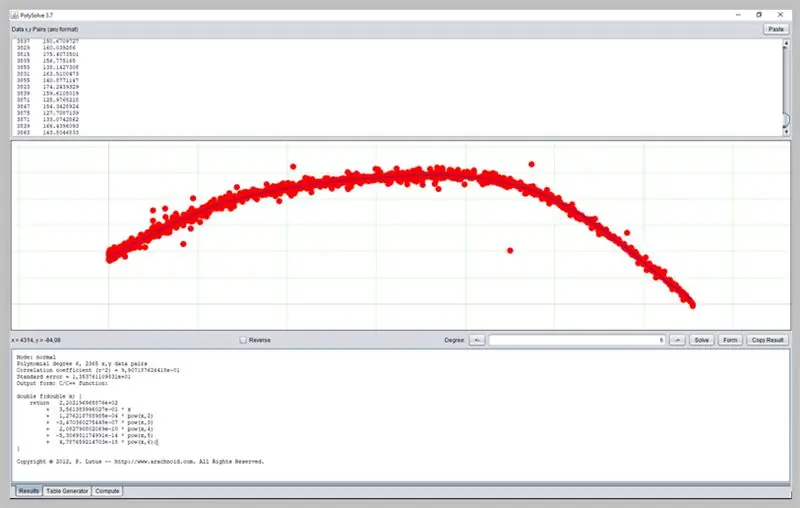
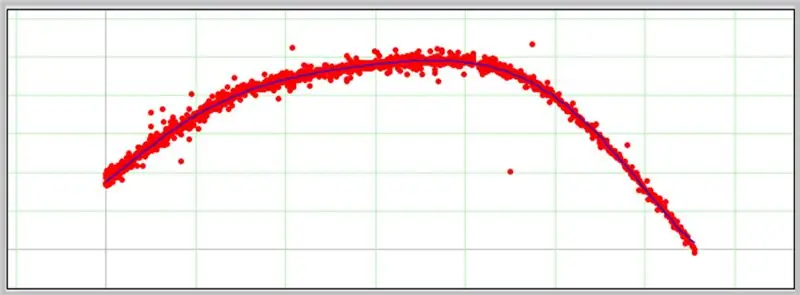
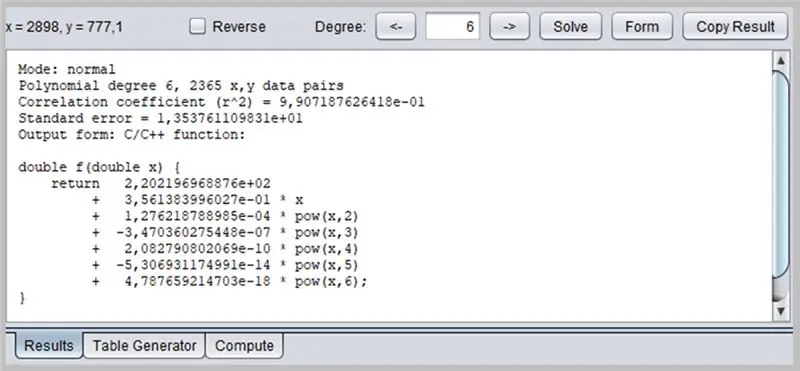
Un alt software interesant pentru determinarea curbelor este PolySolve, care poate fi utilizat direct la link-ul: https://arachnoid.com/polysolve/ sau descărcat ca aplicație Java.

Permite aplicarea regresiilor polinomiale de grad superior și livrarea funcției formatate, precum și a altor funcționalități.

Pentru a-l utiliza, pur și simplu introduceți datele în prima casetă de text. Datele trebuie să urmeze ordinea X, Y separată printr-o virgulă sau o filă. Fii prudent când folosești corect punctul ca punct zecimal.

O diagramă va apărea în caseta următoare dacă datele introduse sunt corect formatate.

Iată cum a decurs curba noastră de eroare ADC.

Această fereastră va prezenta rezultatul regresiei, inclusiv datele de adecvare a funcției, care la rândul lor pot avea ieșirea formatată în mai multe moduri: ca funcție C / C ++, o listă de coeficienți, o funcție scrisă în Java etc.

Notă: Acordați atenție separatoarelor zecimale

Pasul 20: Constante și configurare ()

Amintesc aici GPIO-ul folosit pentru captura analogică. Inițializez portul serial, precum și pinul determinat pentru captura analogică.

const int pin_leitura = 36; // GPIO folosit pentru captura analogică void setup () {Serial.begin (1000000); // Iniciciando a porta serial somente para debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

Pasul 21: Bucla () și funcția de corectare

Realizăm captarea tensiunii ajustate și imprimăm valorile cu sau fără corecțiile corecte.

void loop () {int valor_analogico = analogRead (pin_leitura); // realizează o captură de tensiune ajustată //Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimare os valores for debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor maxim de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor minimum de 0}

Observați în linia 12 că avem opțiunea de a tipări datele cu adăugarea funcției de diferență f (valoare_analogică).

Pasul 22: Utilizarea funcției de corecție PolySolve

Aici, folosim funcția PolySolve din interiorul Arduino IDE.

/ * Mod: grad polinomial normal 6, 2365 x, y perechi de date Coeficient de corelație (r ^ 2) = 9, 907187626418e-01 Eroare standard = 1, 353761109831e + 01 Forma de ieșire: Funcția C / C ++: Copyright © 2012, P. Lutus - https://www.arachnoid.com. Toate drepturile rezervate. * / double f (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Rețineți modificarea virgulă cu punct ca separator zecimal.

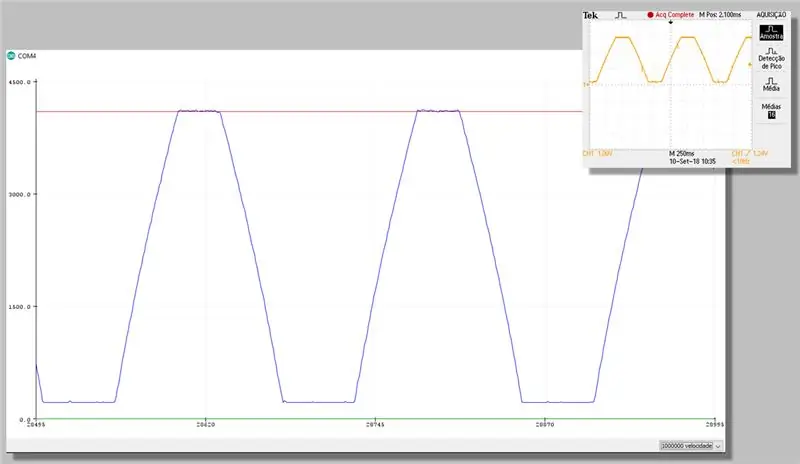
Pasul 23: Captură cu corecție - Plotter Serial

Pasul 24: Costul de calcul

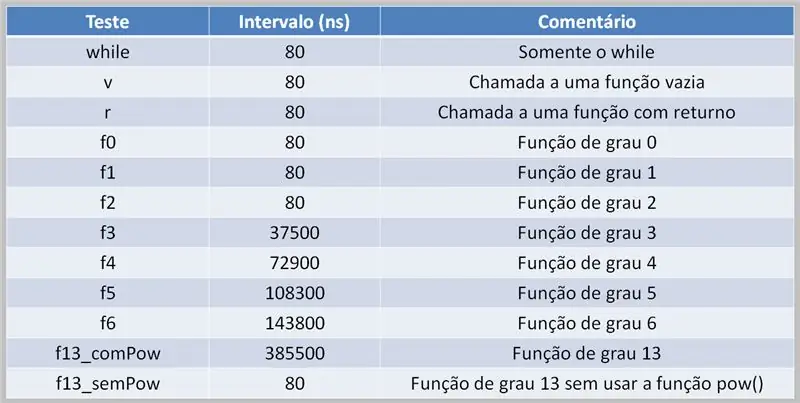
Pentru a efectua calcule polinomiale, este necesar ca procesorul să se ocupe de această sarcină. Acest lucru poate duce la întârzieri în execuție, în funcție de codul sursă și de puterea de calcul disponibilă.

Aici, vedem un tabel de rezultate al unui test care utilizează polinoame cu mai multe grade. Observați diferența dintre momentele în care funcția pow () a fost utilizată și când nu a fost.

Pasul 25: Codul de testare - Setup () și Start Loop ()

Aici avem codul folosit în testul nostru.

void setup () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // quantitate de chamadas float contador = 0,0; // contador de chamadas

Pasul 26: Cod de testare - buclă () și procesare

Am folosit funcția micros () pentru a obține valoarea în microsecunde.

// ============= inicia o proces float agora = micros (); // marca o instante initial while (contador <quantitate) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / quantitate; // determina o intervalo care se trece pentru fiecare iterație // ============= finaliza procesul

Pasul 27: Cod de test - Buclă () - Rezultate

Printăm valoarea returnată din funcția de gradul 13 cu și fără POW pentru comparație, precum și intervalul de procesare.

// imprime o valor returnado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print ("-"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a funtion POW Serial.print ("-"); // imprime o intervalo do processamento Serial.println (agora, 6); }

Pasul 28: Cod de testare - Funcții utilizate

Funcții goale (numai cu returnare) de gradul 0 și 1.

// FUNÇÃO VAZIAdouble v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x; } // FUNÇÃO DE GRAU 0 double f0 (double x) {return 2.202196968876e + 02; } // FUNÇÃO DE GRAU 1 double f1 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x; }

Funcții de gradul 2, 3 și 4.

// FUNÇÃO DE GRAU 2double f2 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 double f3 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3); } // FUNÇÃO DE GRAU 4 double f4 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4); }

Funcții de gradul 5 și 6.

// FUNÇÃO DE GRAU 5double f5 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 double f6 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Funcția de gradul 13 folosind POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

Funcția de gradul 13 fără utilizarea POW.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e-35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Pasul 29: Fișiere

Descărcați fișierele:

PDF

EU NU

Foaie de calcul