Modul de direcție laser DIY pentru Arduino: 14 pași (cu imagini)

2024 Autor: John Day | [email protected]. Modificat ultima dată: 2024-01-30 11:45

În acest Instructable, voi demonstra construcția unui modul de direcție cu fascicul laser cu o singură oglindă cu două axe, utilizând piese imprimate 3D și componente ieftine de la eBay.

Acest proiect are similarități cu Arduino Laser Show cu Full XY Control și Arduino Laser Show cu Real Galvos, dar cred că este primul care folosește un design tipărit 3D cu solenoizi ieftini. Pun toate fișierele de proiectare sub GPLv3, astfel încât proiectarea să poată fi îmbunătățită și îmbunătățită.

Deși în prezent am asamblat doar modulul și am scris un cod de test foarte de bază, speranța mea este că într-o zi îl voi putea trece la nivelul următor prin încorporarea codului de grafică vectorială din tensiunea analogică super rapidă instructabilă, super rapidă de la Arduino.

Pasul 1: Adunați părțile imprimate 3D

Ansamblul laser constă din următoarele părți:

• 4 micro solenoizi
• O oglindă de 1/2 inch
• Patru șuruburi M3

Solenoizii pe care i-am folosit au fost cumpărați de pe eBay cu 1,45 USD fiecare. Oglinda rotundă a fost găsită în culoarul de artizanat de la HobbyLobby - un pachet de 25 m-a costat mai puțin de 3 dolari. De asemenea, puteți găsi oglinzi pe eBay.

De asemenea, veți avea nevoie de un indicator laser ieftin, din nou, de la eBay. Un laser violet împreună cu o foaie de vinil strălucitor în întuneric este o combinație excelentă pentru acest proiect!

Un set de mâini ajutătoare nu este necesar, dar va fi foarte util pentru ținerea și poziționarea indicatorului laser. O clemă mare pentru liant poate fi utilizată pentru a ține apăsat butonul de alimentare.

Veți avea nevoie de un Arduino (eu am folosit un Arduino Nano) și o modalitate de a conduce solenoizii. Așa cum a afirmat VajkF în comentarii, puteți utiliza un H-bridge prefabricat, cum ar fi cele bazate pe L298 sau L9110. Acestea sunt disponibile pe eBay pentru câțiva dolari și pot fi folosite și pentru acționarea motoarelor și a proiectelor de robotică.

Deoarece nu aveam un pod H, mi-am construit propriul driver din componente discrete:

• Patru tranzistori bipolari NPN (am folosit un MPS3704)
• Patru rezistențe (am folosit rezistor de 1,2 k ohm)
• Patru diode (am folosit un 1N4004)
• O baterie de 9V și un conector pentru baterie

Componentele electronice provin de la laboratorul meu, deci nu am un cost exact pentru ele, dar dacă nu aveți deja piesele sau le puteți elimina, este probabil mai rentabil să utilizați un H-bridge pre-construit. Cu toate acestea, voi oferi schemele pentru construirea propriei dvs.

Pasul 2: Imprimați 3D modulul de direcție în oglindă

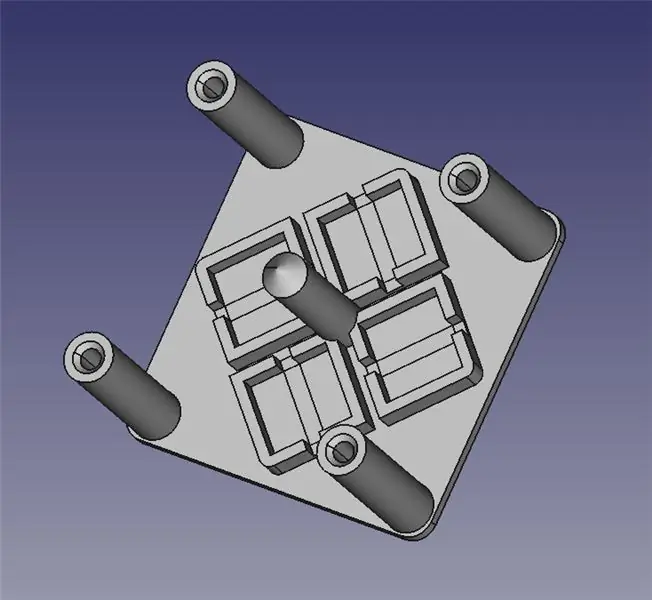
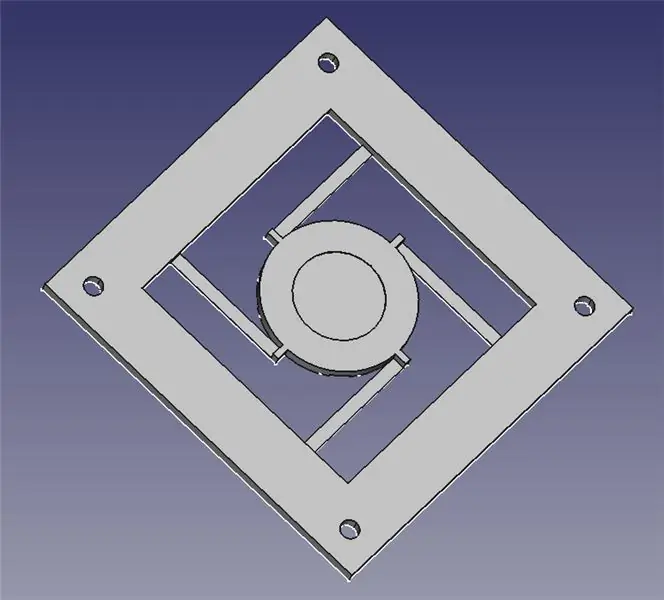
Modulul de direcție laser constă din două părți imprimate 3D: o bază pentru montarea a patru solenoide și o platformă articulată pentru oglindă.

Am atașat cele două fișiere STL pentru dvs. la imprimarea 3D, precum și fișierele FreeCAD în cazul în care trebuie să modificați designul. Tot conținutul se află sub GPLv3, deci sunteți liber să faceți și să împărtășiți îmbunătățirile dvs.!

Pasul 3: Asamblați modulul laser

• Folosiți adeziv fierbinte pentru a fixa cei patru solenoizi pe piesa inferioară.
• Folosiți adeziv fierbinte pentru a fixa oglinda pe centrul piesei superioare.
• Introduceți pistoanele metalice în solenoizi și apoi poziționați piesa superioară pe stâlpi (dar nu o înșurubați). Rotiți ușor partea superioară și, cu ajutorul unei șurubelnițe mici, ridicați fiecare piston în poziție. Buza discului trebuie să alunece în canelura pistonului. Aveți grijă, deoarece balamalele imprimate 3D sunt foarte fragile. Cu răbdare și, eventual, câteva încercări eșuate, ar trebui să puteți poziționa toate cele patru pistoane fără a răsuci sau a exercita presiuni pe balamale.
• Odată ce toate pistoanele sunt poziționate, introduceți parțial șuruburile M3, dar înainte de a le strânge în jos, împingeți ușor pe fiecare piston ușor și asigurați-vă că oglinda se înclină liber. Dacă nu se mișcă liber sau se prinde, poate fi necesar să scoateți placa superioară, să scoateți unul sau mai multe solenoide libere și să o atașați din nou la un unghi ușor exterior (punerea distanțierelor între ea și stâlpul central poate ajuta la acest lucru).

Pasul 4: Imprimați colierul indicatorului laser

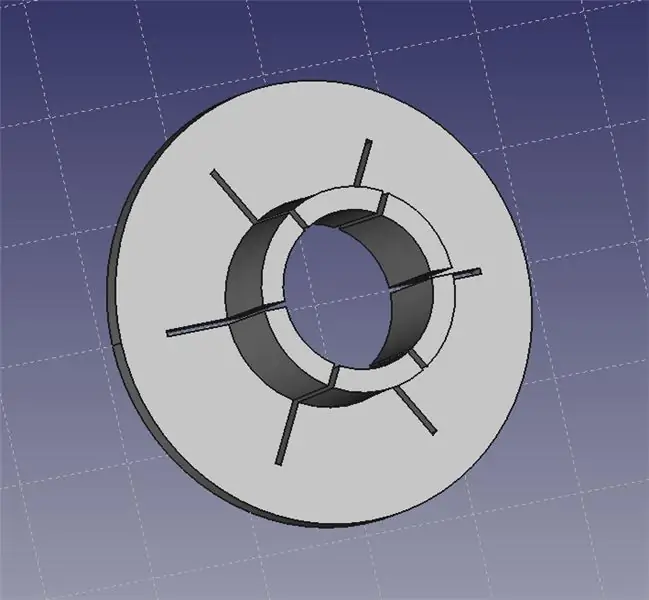
Gulerul indicatorului laser se potrivește pe capul indicatorului laser. Puteți utiliza apoi un set de mâini ajutătoare pentru a apuca gulerul și a vă permite să poziționați laserul exact pe banca dvs.

Pasul 5: Asamblați circuitul de conducere

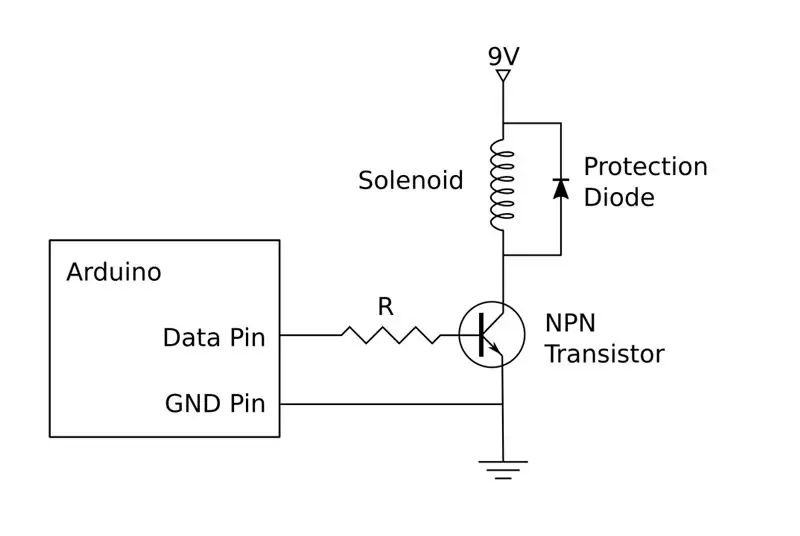
Circuitul de acționare este prezentat în schemă. După cum sa menționat mai devreme, versiunea mea este construită din componente discrete, dar puteți utiliza, de asemenea, un H-bridge ușor disponibil. Dacă alegeți să vă construiți propriul, va trebui să construiți patru copii ale acestui circuit, câte unul pentru fiecare dintre cele patru solenoide.

Fiecare circuit se va conecta la un pin Arduino, două pentru controlul solenoidului stâng și drept și două pentru solenoidele sus și jos. Acestea vor trebui conectate la pinii capabili PWM, astfel:

• Pinul 9: solenoid sus
• Pinul 3: Solenoid de jos
• Pinul 11: Solenoid stâng
• Pinul 10: Solenoidul drept

O singură baterie de 9V poate fi utilizată pentru conducerea tuturor celor patru circuite ale driverului solenoid sau puteți utiliza o sursă de alimentare de pe bancă. Arduino va rula alimentarea USB și nu ar trebui să fie conectat la partea pozitivă a bateriei de 9V. Cu toate acestea, partea negativă a bateriei este utilizată ca referință la sol și ar trebui să fie conectată la pinul GND de pe Arduino, precum și la pinii emițătorului de pe tranzistoare.

Pasul 6: încărcați exemplul de cod

Exemplul de cod a fost actualizat cu următoarele caracteristici:

• Reglează frecvența PWM astfel încât mecanismul să fie aproape silențios la viteze mici. Zgomotul din Motion Test 1 a dispărut în totalitate!
• Se adaugă ca ecuații de tensiune pe baza hârtiei de către Schimpf pentru a „lineariza” răspunsul neliniar al solenoizilor.

De asemenea, am inclus o implementare a unui Lorenz Attractor bazat pe codul de pe acest blog.

Fidelitatea rezultatelor lasă de dorit, dar încă lucrez la asta!:)

Pașii ulteriori ilustrează unele dintre tehnicile utilizate în cod.

Pasul 7: Reducerea volumului

În Testul meu de mișcare 1, puteți auzi un bâzâit puternic, în special în timpul mișcării în sus și în jos. Se pare că acest lucru a fost cauzat de frecvența implicită de tăiere PWM a Arduino aflându-se în intervalul sonor. Pornirea și oprirea rapidă a tensiunii bobinei le-ar face să vibreze la acea frecvență, transformându-le în mici difuzoare.

Pentru a rezolva această problemă, am crescut frecvența PWM în cod:

#define PWM_FREQ_31372Hz 0x01 // Setează frecvența PWM la 31372,55 Hz # define PWM_FREQ_3921Hz 0x02 // Setează frecvența PWM la 3921,16 Hz #define PWM_FREQ_980Hz 0x03 // Setează frecvența PWMt & 0b11111000) | frecvență; // Setați timer1 (pinii 9 și 10) frecvența TCCR2B = (TCCR2B și 0b11111000) | frecvență; // Setați timer2 (pinii 3 și 11) frecvența}

Setarea frecvenței Arduino PWM este un truc util pentru a reduce liniile solenoidelor sau motoarelor. Experimentați cu diferitele opțiuni de frecvență pentru a vedea care dintre acestea vă oferă cele mai bune rezultate. Deși implică o programare mai avansată, o resursă bună despre modul de funcționare a temporizatoarelor este aici.

Pasul 8: Reglarea tensiunilor pentru a reduce distorsiunea

Testele mele inițiale de mișcare au arătat că au fost distorsiuni semnificative în răspunsul solenoizilor. În Motion Test 3 (figura din stânga), ceea ce trebuia să fie o spirală circulară a devenit în schimb o rețea dreptunghiulară cu margini zimțate.

Rezolvarea acestei probleme a necesitat un pic de matematică, dar am reușit să găsesc o hârtie uimitoare pe web care m-a ajutat să înțeleg problema suficient de bine pentru a o rezolva în software.

Ceea ce urmează vă pasează prin procesul pe care l-am parcurs pentru a regla sistemul și a îmbunătăți aspectul urmelor rezultate!

Pasul 9: Perfecționarea software-ului, cu matematică

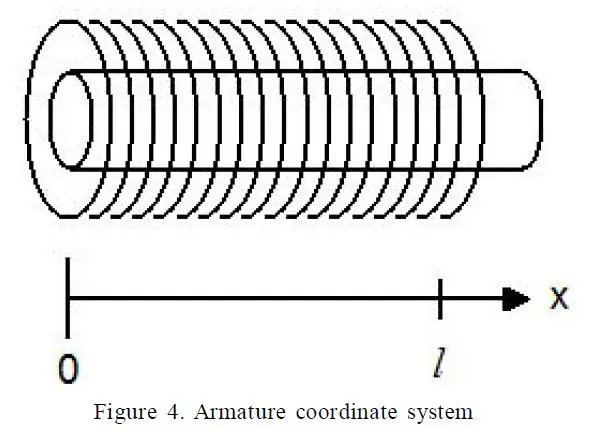
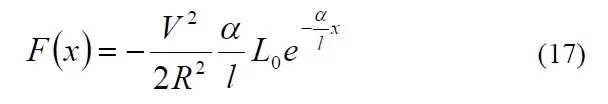
Secretul reglării sistemului s-a dovedit a fi o lucrare excelentă numită „O explicație detaliată a forței solenoidei” de Paul H. Schimpf de la Universitatea din Washington (legătură). În special, ecuația 17 mi-a dat forța solenoidă în termeni diferiți.

Următorii termeni au fost ușor de măsurat:

• R - Rezistența solenoidului meu
• l - Lungimea solenoidului
• x - Deplasarea pistonului în solenoid
• V - Tensiunea pe solenoid

Știam, de asemenea, că forța produsă de solenoid trebuia să echilibreze forța din arcurile imprimate 3D de pe oglinda cu două axe. Forța unui izvor este guvernată de legea lui Hooke, care se afirmă după cum urmează:

F = -kx

Deși nu știam valoarea lui k, măcar știam că forța pe care am ieșit-o din ecuația 17 din lucrarea lui Schimpf trebuia să egaleze forța din legea lui Hooke.

Valoarea alfa (α) a fost una dificilă. Deși ecuațiile 13 și 14 au arătat cum să se calculeze aceste valori din aria solenoidului (A), numărul de rotații (N) și valorile permeabilității magnetice (μ), nu am vrut să trebuiască să rup un solenoid pentru a număra numărul de rotații și nici nu știam materialul din care a fost realizat miezul solenoidului.

Pasul 10: un tester de componente ieftin salvează ziua

Sa dovedit totuși că ecuația 15 și 16 mi-a oferit ceea ce aveam nevoie. Aveam un tester de componente M328 ieftin pe care îl cumpărasem de la eBay pentru 10 USD. A fost capabil să-l folosească pentru a măsura inductanța solenoidului meu și am constatat că prin împingerea armăturii la adâncimi diferite mi-a dat valori de inducție diferite.

Măsurarea acestuia cu armătura complet introdusă mi-a dat valoarea L (0).

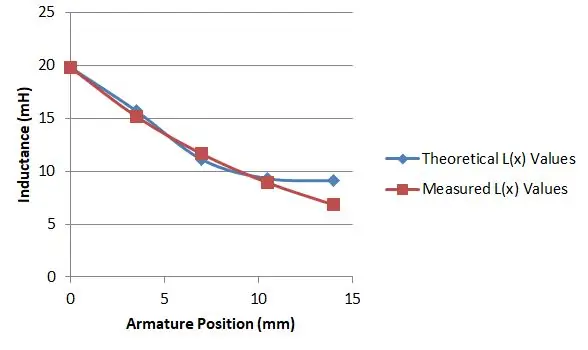
Lungimea solenoidului meu a fost de 14 mm, așa că am măsurat inductanța cu armătura în cinci poziții și acest lucru mi-a dat diferite valori pentru L (x):

• L (0,0) = 19,8 mH
• L (3,5) = 17,7 mH
• L (7,0) = 11,1 mH
• L (10,5) = 9,3 mH
• L (14) = 9,1 mH

Apoi am folosit o foaie de calcul pentru a trasa valorile mele față de valoarea ecuației 15 și 16, pentru o anumită alegere a μr și apoi am modificat alegerea mea până când am găsit o potrivire bună. Acest lucru s-a întâmplat când μr era 2,9, așa cum se arată în grafic.

Pasul 11: Găsiți constanta de primăvară K, rezolvați problema

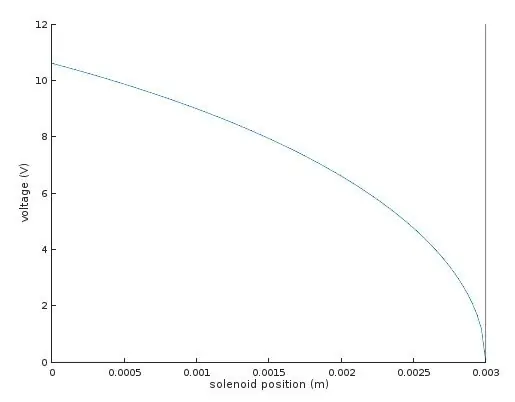
Singura necunoscută rămasă a fost K, constanta primăverii. Am măsurat acest lucru aplicând 9V la unul dintre solenoizii din ansamblul meu cu două axe și măsurând distanța în care oglinda a fost trasă în jos. Cu aceste valori, am putut rezolva ecuațiile pentru K, care am găsit că este în jur de 10,41.

Acum aveam valorile de care aveam nevoie pentru a calcula tragerea solenoidului în diferite poziții de-a lungul cursei. Prin setarea F (x) egală cu forța arcului din legea lui Hooke, pot rezolva tensiunea necesară V.

Graficul arată tensiunea necesară pentru deplasarea solenoidului în orice poziție dorită x.

În dreapta, unde tensiunea este zero și poziția este de 3 mm, aceasta corespunde punctului de repaus neutru al solenoidului atunci când balamalele imprimate 3D sunt complet relaxate. Deplasarea la stânga pe grafic corespunde tragerii armăturii în solenoid împotriva tragerii balamalelor imprimate 3D - acest lucru necesită inițial mai multă tensiune, dar pe măsură ce armătura devine mai adâncă în solenoid, tracțiunea crește și tensiunea de conducere necesară se diminuează.

Această relație este cu siguranță neliniară, dar cu ecuațiile din hârtia lui Schimpf, pot scrie codul meu Arduino pentru a transmite tensiunile corecte, astfel încât deviația fasciculului să fie liniară:

float positionToVoltage (float x) {

// Restabilirea forței exercitate de balamale (Legea lui Hooke) la x dorit. const float spring_F = -spring_K * (x - spring_X0); // Tensiune astfel încât forța de tragere a solenoidului să se potrivească cu // forța de refacere a balamalelor returnează sqrt (-2 * R * R * (- arc_F) * solenoid_len / (a * L_0 * exp (-a * x / solenoid_len))); }

Acest lucru duce la o spirală mult mai circulară decât în testul meu original de mișcare. Misiune indeplinita!

Pasul 12: Întrebare și răspunsuri despre circuitul driverului folosind componente discrete

De ce nu pot conecta solenoidul direct la Arduino?

Este o chestiune de cât de mult curent poate furniza Arduino fără a suferi daune. Aceasta este de aproximativ 40mA pe pin. Știind că Arduino funcționează la 5V, putem folosi legea lui Ohm pentru a calcula rezistența minimă necesară a sarcinii (în acest caz, solenoidul). Împărțirea a 5 volți la 0,040 amperi ne oferă 125 ohmi. Dacă sarcina are o rezistență mai mare, o putem conecta direct la Arduino, altfel nu putem. Un solenoid mic are de obicei o rezistență de 50 ohmi, deci nu îl putem conduce direct de pe Arduino. Dacă am face-o, ar trage 100mA, ceea ce este clar prea mult.

De ce folosești 9V pentru solenoid, dar 5V pentru Arduino?

Arduino funcționează la 5V, dar acest lucru este puțin prea mic pentru un solenoid. Utilizarea unui tranzistor ne permite să alegem o tensiune pentru solenoid, care este independentă de 5V utilizată pentru Arduino.

De unde știu dacă un tranzistor este potrivit pentru acest proiect?

La fel ca Arduino, cerința majoră este ca curentul care curge prin solenoid să nu depășească valorile maxime ale tranzistorului (în special, curentul colectorului). Putem calcula cu ușurință cel mai rău scenariu măsurând rezistența solenoidului și apoi împărțind tensiunea de alimentare la aceasta. În cazul unui curent de alimentare de 9V pentru solenoizi și a unei rezistențe a solenoidului de 50 ohmi, cel mai rău scenariu ne situează la 180mA. MPS3704, de exemplu, este evaluat pentru un curent maxim de colector de 600 mA, ceea ce ne oferă o marjă de aproximativ 3.

Cum pot determina valoarea minimă a rezistenței de pus între ieșirea Arduino și baza tranzistorului?

Ieșirea Arduino va conecta piciorul de bază al tranzistoarelor bipolare printr-un rezistor de limitare a curentului. Deoarece Arduino funcționează la 5V, putem folosi din nou legea lui Ohm pentru a calcula rezistența necesară pentru a limita curentul sub 40mA. Adică, împărțiți 5 volți la 0,04 amperi pentru a obține o valoare de cel puțin 125 ohmi. Valorile mai mari ale rezistorului vor reduce curentul, oferindu-ne astfel o marjă de siguranță și mai mare.

Există o valoare maximă pentru acea rezistență pe care nu ar trebui să o depășesc?

Se pare, da. Un tranzistor are ceea ce este cunoscut sub numele de câștig de curent. De exemplu, dacă câștigul este de 100, înseamnă că, dacă punem 1mA în bază, atunci până la 100mA vor curge prin sarcina pe care tranzistorul o controlează. Dacă punem 1,8mA în bază, atunci până la 180mA vor curge prin sarcină. Deoarece am calculat mai devreme că la 9V, 180mA curge prin solenoid, atunci un curent de bază de 1,8mA este „punctul dulce” și mai puțin, iar solenoidul nostru nu se va aprinde complet.

Știm că Arduino scoate 5V și vrem să curgă 1,8 mA de curent, așa că folosim legea lui Ohm (R = V / I) pentru a calcula rezistența (R = V / I). 5V împărțit la 1,8mA oferă o rezistență de 2777 ohmi. Prin urmare, având în vedere ipotezele pe care le-am făcut, ne așteptăm ca rezistența să se situeze între 125 și 2777 - alegerea a ceva de genul 1000 ohmi ne oferă o marjă de siguranță destul de bună în ambele sensuri.

Pasul 13: Analiza problemelor actuale și a soluțiilor posibile

Prototipul actual prezintă potențial, dar rămân câteva probleme:

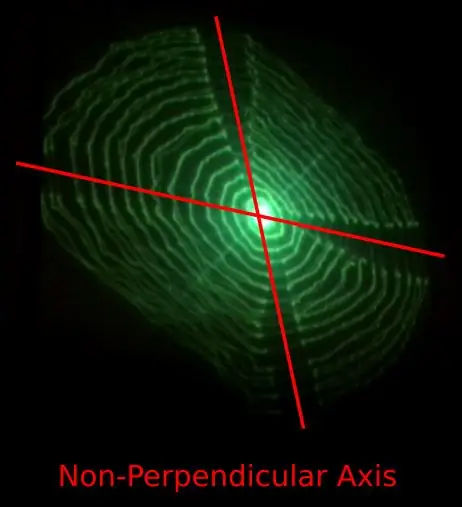
1. Mișcarea de-a lungul axelor X și Y nu pare a fi perpendiculară.
2. Se produce un salt când oglinda își schimbă direcția.
3. Rezoluția este destul de scăzută și există modele de trepte vizibile.
4. La viteze mai mari de mișcare, calea laserului este distorsionată de vibrații și sunete.

Problema 1) poate fi cauzată de proiectarea balamalelor flexibile imprimate 3D care transmit mișcare de-a lungul unei axe către axa perpendiculară.

Problema 2) se datorează slăbirii cuplajului dintre pistoanele de acționare și platforma oglinzii, ceea ce face ca oglinda să se smucească și să sară la tranziții între axa X și Y. Această mișcare bruscă duce la un decalaj întunecat în formă de X în care punctul laser face o mișcare necontrolată mai rapidă.

Problema 3) apare deoarece implicit Arduino PWM are doar 255 de niveluri și destul de multe dintre acestea sunt irosite datorită formei curbei de tensiune. Acest lucru ar putea fi îmbunătățit semnificativ prin utilizarea timer1, care este de 16 biți și ar putea avea 65536 de valori unice.

Problema 4) apare deoarece oglinda și armătura glisantă a solenoidului (pistoanele) constituie o cantitate semnificativă de masă în mișcare.

Deoarece problemele 1) și 2) sunt legate de proiectarea mecanică, o posibilitate poate fi îndepărtarea pistoanelor metalice și înlocuirea acestora cu magneți mici de pământ rar care sunt atașați direct pe placa de înclinare. Solenoizii ar fi o bobină deschisă care ar atrage sau respinge magneții fără a face contact fizic. Acest lucru ar duce la o mișcare mai lină și ar elimina posibilitatea de sacadări, reducând în același timp masa totală.

Reducerea masei este soluția principală pentru problema 4), dar orice probleme rămase ar putea fi direcționate direct în software prin implementarea unui profil de control al mișcării în software pentru a accelera și a decelera oglinda într-un mod controlat. Acest lucru se face deja pe scară largă în firmware-ul imprimantei 3D și metode similare ar putea funcționa și aici. Iată câteva resurse legate de controlul mișcării, deoarece se aplică imprimantelor 3D:

• „Matematica profilurilor de control al mișcării”, Chuck Lewin (link)
• „Mișcarea controlată a fost explicată”, (link)

Bănuiesc că adăugarea unui profil de control al mișcării trapezoidale ar permite ca oglinda să fie condusă la viteze mult mai mari, fără a suna sau a artefacte de vibrații.

Pasul 14: Lucrări viitoare și aplicații posibile

Deși dezvoltarea de soluții la aceste probleme va necesita o cantitate considerabilă de muncă, sper că acest modul open-source de direcție a fasciculului poate deveni o alternativă accesibilă la proiectele bazate pe galvanometru în aplicații precum:

• Un spectacol laser ieftin pentru DJ și VJ.
• Un afișaj vectorial electromecanic pentru un joc arcade de epocă, cum ar fi Vectrex.
• O imprimantă SLA 3D tip rășină DIY care, în spiritul mișcării RepRap, poate imprima propriul modul de direcție laser.
• Panoramare digitală sau stabilizare optică a imaginii pentru camere.

Premiul II la Concursul Arduino 2017